题目内容
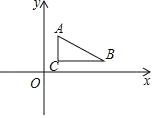
【题目】已知,如图,A点坐标是(1,3),B点坐标是(5,1),C点坐标是(1,1)
(1)求△ABC的面积是____;
(2)求直线AB的表达式;
(3)一次函数y=kx+2与线段AB有公共点,求k的取值范围;
(4)y轴上有一点P且△ABP与△ABC面积相等,则P点坐标是_____.
【答案】(1)4;(2)y=﹣![]() x+
x+![]() ;(3)0<k≤1或﹣
;(3)0<k≤1或﹣![]() ≤k<0;(4)(0,
≤k<0;(4)(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)根据A、B、C三点的坐标可得AC=3﹣1=2,BC=5﹣1=4,∠C=90°,再利用三角形面积公式列式计算即可;
(2)设直线AB的表达式为y=kx+b.将A(1,3),B(5,1)代入,利用待定系数法即可求解;
(3)由于y=kx+2是一次函数,所以k≠0,分两种情况进行讨论:①当k>0时,求出y=kx+2过A(1,3)时的k值;②当k<0时,求出y=kx+2过B(5,1)时的k值,进而求解即可;
(4)过C点作AB的平行线,交y轴于点P,根据两平行线间的距离相等,可知△ABP与△ABC是同底等高的两个三角形,面积相等.根据直线平移k值不变可设直线CP的解析式为y=﹣![]() x+n,将C点坐标代入,求出直线CP的解析式,得到P点坐标;再根据到一条直线距离相等的直线有两条,可得另外一个P点坐标.
x+n,将C点坐标代入,求出直线CP的解析式,得到P点坐标;再根据到一条直线距离相等的直线有两条,可得另外一个P点坐标.
解:(1)∵A点坐标是(1,3),B点坐标是(5,1),C点坐标是(1,1),
∴AC=3﹣1=2,BC=5﹣1=4,∠C=90°,
∴S△ABC=![]() ACBC=
ACBC=![]() ×2×4=4.
×2×4=4.
故答案为4;
(2)设直线AB的表达式为y=kx+b.
∵A点坐标是(1,3),B点坐标是(5,1),
∴![]() ,解得
,解得 ,
,
∴直线AB的表达式为y=﹣![]() x+
x+![]() ;
;
(3)当k>0时,y=kx+2过A(1,3)时,
3=k+2,解得k=1,
∴一次函数y=kx+2与线段AB有公共点,则0<k≤1;
当k<0时,y=kx+2过B(5,1),
1=5k+2,解得k=﹣![]() ,
,
∴一次函数y=kx+2与线段AB有公共点,则﹣
综上,满足条件的k的取值范围是0<k≤1或﹣![]() ≤k<0;
≤k<0;
(4)过C点作AB的平行线,交y轴于点P,此时△ABP与△ABC是同底等高的两个三角形,所以面积相等.
设直线CP的解析式为y=﹣![]() x+n,
x+n,
∵C点坐标是(1,1),
∴1=﹣![]() +n,解得n=
+n,解得n=![]() ,
,
∴直线CP的解析式为y=﹣![]() x+
x+![]() ,
,
∴P(0,![]() ).
).
设直线AB:y=﹣![]() x+
x+![]() 交y轴于点D,则D(0,
交y轴于点D,则D(0,![]() ).
).
将直线AB向上平移![]() ﹣
﹣![]() =2个单位,得到直线y=﹣
=2个单位,得到直线y=﹣![]() x+
x+![]() ,与y轴交于点P′,此时△ABP′与△ABP是同底等高的两个三角形,所以△ABP与△ABC面积相等,易求P′(0,
,与y轴交于点P′,此时△ABP′与△ABP是同底等高的两个三角形,所以△ABP与△ABC面积相等,易求P′(0,![]() ).
).
综上所述,所求P点坐标是(0,![]() )或(0,
)或(0,![]() ).
).
故答案为(0,![]() )或(0,
)或(0,![]() ).
).