题目内容
已知:在Rt△ABC中,∠C=90°,CD⊥AB于D,∠A=60°,CD=![]() ,线段AB长为( )。
,线段AB长为( )。
A.2 B.3 C.4 D.3![]()
 |
C
分析:欲求AB,可由AB=BD+AD,分别在两个三角形中利用勾股定理和特殊角,求出BD和AD。或欲求AB,可由![]() ,分别在两个三角形中利用勾股定理和特殊角,求出AC和BC。
,分别在两个三角形中利用勾股定理和特殊角,求出AC和BC。
详细解答:在Rt△ACD中,∠A=60°,那么∠ACD=30°,又已知CD=![]() ,所以利用勾股定理或特殊三角形的三边的比求出AD=1。
,所以利用勾股定理或特殊三角形的三边的比求出AD=1。
在Rt△ACB中,∠A=60°,那么∠B=30°。
在Rt△BCD中,∠B=30°,又已知CD=![]() ,所以BC=2
,所以BC=2![]() ,利用勾股定理或特殊三角形的三边的比求出BD=3。
,利用勾股定理或特殊三角形的三边的比求出BD=3。
因此AB=BD+CD=3+1=4,

练习册系列答案
相关题目
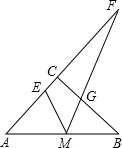 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.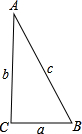 已知:在Rt△ABC中,∠C=90°,∠A=30°,b=
已知:在Rt△ABC中,∠C=90°,∠A=30°,b=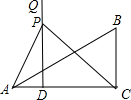 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.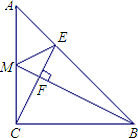 已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.
已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB. 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.