题目内容
 如图,∠ACB=∠DFE,BC=EF,要使△ABC≌△DEF,则需要补充一个条件,这个条件可以是
如图,∠ACB=∠DFE,BC=EF,要使△ABC≌△DEF,则需要补充一个条件,这个条件可以是
- A.AB=DE
- B.∠ABC=∠DEF
- C.BF=EC
- D.∠ACE=∠DFB
B
分析:全等三角形的判定定理有SAS,ASA,AAS,SSS,看看各个选项是否符合条件,即可判断出选项.
解答:A、根据AB=DE,BC=EF,∠ACB=∠DFE不能推出△ABC≌△DEF,故本选项错误;
B、∵在△ABC和△DEF中
 ,
,
∴△ABC≌△DEF(ASA),故本选项正确;
C、∵BF=EC,
∴BF-CF=EC-CF,
∴BC=EF,即具备条件BC=EF和∠ACB=∠DFE不能推出△ABC≌△DEF,故本选项错误;
D、根据∠ACE=∠DFB,不能推出△ABC和△DEF的第三个条件相等,即具备条件BC=EF和∠ACB=∠DFE不能推出△ABC≌△DEF,故本选项错误;
故选B.
点评:本题考查了全等成三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,即要证两三角形全等,必须具备相等的三个条件,且这三个条件满足SAS,ASA,AAS,SSS.
分析:全等三角形的判定定理有SAS,ASA,AAS,SSS,看看各个选项是否符合条件,即可判断出选项.
解答:A、根据AB=DE,BC=EF,∠ACB=∠DFE不能推出△ABC≌△DEF,故本选项错误;
B、∵在△ABC和△DEF中
 ,
,∴△ABC≌△DEF(ASA),故本选项正确;
C、∵BF=EC,
∴BF-CF=EC-CF,
∴BC=EF,即具备条件BC=EF和∠ACB=∠DFE不能推出△ABC≌△DEF,故本选项错误;
D、根据∠ACE=∠DFB,不能推出△ABC和△DEF的第三个条件相等,即具备条件BC=EF和∠ACB=∠DFE不能推出△ABC≌△DEF,故本选项错误;
故选B.
点评:本题考查了全等成三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,即要证两三角形全等,必须具备相等的三个条件,且这三个条件满足SAS,ASA,AAS,SSS.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
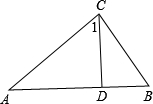 如图,△ACB中,∠ACB=90°,∠1=∠B.
如图,△ACB中,∠ACB=90°,∠1=∠B. 13、如图,∠ACB=90°,把Rt△ABC绕点A逆时针旋转90°得到Rt△AB1C1,若BC=1,AB=2,则∠CAB1的度数是
13、如图,∠ACB=90°,把Rt△ABC绕点A逆时针旋转90°得到Rt△AB1C1,若BC=1,AB=2,则∠CAB1的度数是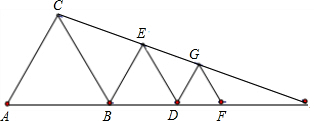 如图,△ACB、△BDE和△DGF都是等边三角形,且点E、G在△ABC边AB的延长线上,设等边的面积分别为S1、S2、S3,若S1=9,S3=1,则S2=
如图,△ACB、△BDE和△DGF都是等边三角形,且点E、G在△ABC边AB的延长线上,设等边的面积分别为S1、S2、S3,若S1=9,S3=1,则S2= 如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2.3cm,则BE的长为
如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2.3cm,则BE的长为 已知:如图,∠ACB=∠DBC,根据图形条件,若增加一个条件
已知:如图,∠ACB=∠DBC,根据图形条件,若增加一个条件