��Ŀ����
��ֱ������ϵxOy�У�������y=x2-2tx+t2-t��t��0����x�����������ֱ�ΪA��B��A��B����ߣ���ֱ��l��y=kx���������ߵĶ���C���������ߵ���һ������ΪD����1���������ߵĶ���C�����꣨�ú�t�Ĵ�����ʾ���������ֱ��l �Ľ���ʽ��
��2����ͼ�٣���t=
| 1 |
| 4 |
��3����t��1ʱ�����ABC�����ΪS1����ABD�����ΪS2���ú�t�Ĵ���ʽ��ʾ
| S1 |
| S2 |
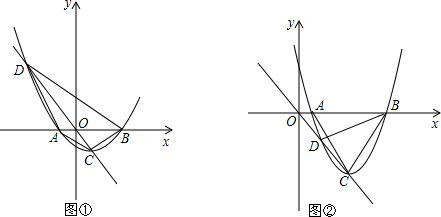
��������1���Ȱ������ȵĽ���ʽ��Ϊ����ʽ����ʽ������䶥�����꣬�ٰ��䶥���������y=kx�������k��ֵ���������ֱ��l�Ľ���ʽ��
��2����t=
���������߽���ʽy=��x-t��2-t�У���y=��x-
��2-
����y=0�������A��B��������꣬�Ѵ������ߵĽ���ʽ��ֱ��l�Ľ���ʽ���������C��D��������꣬����tan��DBA=tan��CAB=
�ɵó���DBA=��CAB����ƽ���ߵ��ж�������֪AC��BD��
��3���ɡ�ABC����ABDͬ��֪
=|
|����ֱ��l�������ߵĽ���ʽ�������x1��x2��ֵ������ֱ�߽���ʽ�ɵó�yC��yD��ֵ�������ɵó����ۣ�
��2����t=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
��3���ɡ�ABC����ABDͬ��֪
| S1 |
| S2 |
| yC |
| yD |
����⣺��1��y=x2-2tx+t2-t=��x-t��2-t��
�ඥ��C������Ϊ��t��-t����
��y=kx���������ߵĶ���C��
�ཫ��C����y=kx����-t=kt��
��t��0��
��k=-1��
��ֱ��l�Ľ���ʽΪy=-x��
��2����t=
���������߽���ʽy=��x-t��2-t�У���y=��x-
��2-
����y=0����ã�x1=
��x2=-
��
��A��-
��0����B��
��0��
��������
����ã�x1=-
��x2=
��
��C��
��-
����D��-
��
��
��tan��DBA=tan��CAB=
��
���DBA=��CAB��
��AC��BD��
��3���ߡ�ABC����ABDͬ�ף�
��
=|
|
��������
��
���x1=t��x2=t-1��
��yC=-t��yD=1-t��
��
=|
|=|
|=
��
�ඥ��C������Ϊ��t��-t����
��y=kx���������ߵĶ���C��
�ཫ��C����y=kx����-t=kt��
��t��0��
��k=-1��
��ֱ��l�Ľ���ʽΪy=-x��
��2����t=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
��A��-
| 1 |
| 4 |
| 3 |
| 4 |
��������
|
| 3 |
| 4 |
| 1 |
| 4 |
��C��
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
��tan��DBA=tan��CAB=
| 1 |
| 2 |
���DBA=��CAB��
��AC��BD��
��3���ߡ�ABC����ABDͬ�ף�
��
| S1 |
| S2 |
| yC |
| yD |
��������
|
���x1=t��x2=t-1��
��yC=-t��yD=1-t��
��
| S1 |
| S2 |
| yC |
| yD |
| -t |
| 1-t |
|
���������⿼����Ƕ��κ����ۺ��⣬�漰�������ε������ʽ�����������������ʡ�ƽ���ߵ��ж��������漰��Ϲ㣬�ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ

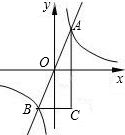 ��ֱ������ϵxoy�У�����y=4x��ͼ���뷴��������y=
��ֱ������ϵxoy�У�����y=4x��ͼ���뷴��������y= ��2012•������ģ����֪����ͼ����ֱ������ϵxOy�У���A��8��0����B��0��6������C��x��ĸ������ϣ�AB=AC������M��x���ϴӵ�C���A�ƶ�������N���߶�AB�ϴӵ�A���B�ƶ�����M��Nͬʱ���������ƶ����ٶȶ�Ϊÿ��1����λ���ƶ�ʱ��Ϊt�루0��t��10����
��2012•������ģ����֪����ͼ����ֱ������ϵxOy�У���A��8��0����B��0��6������C��x��ĸ������ϣ�AB=AC������M��x���ϴӵ�C���A�ƶ�������N���߶�AB�ϴӵ�A���B�ƶ�����M��Nͬʱ���������ƶ����ٶȶ�Ϊÿ��1����λ���ƶ�ʱ��Ϊt�루0��t��10���� ��ʽΪy=x2-mx+n������x2-mx+n=0������������Ϊ-4��
��ʽΪy=x2-mx+n������x2-mx+n=0������������Ϊ-4��