题目内容
梯形ABCD,AD∥BC,∠B=90°,CD>AD+BC,以CD为直径的圆与直线AB的位置关系是
- A.相离
- B.相切
- C.相交
- D.无法确定
C
分析:设CD中点为O,作OF⊥AB于F,比较出OF和半径的关系即可.
解答: 解:如图:设CD中点为O,作OF⊥AB于F,
解:如图:设CD中点为O,作OF⊥AB于F,
∵OF= (AD+BC)(梯形中位线定理)
(AD+BC)(梯形中位线定理)
又∵CD>AD+BC
∴OF= (AD+BC)<
(AD+BC)< CD.
CD.
故⊙O与AB相交.
故选C.
点评:本题考查了直线和圆的位置关系,利用中位线定理比较出AB到圆心的距离与半径的关系是解题的关键.
分析:设CD中点为O,作OF⊥AB于F,比较出OF和半径的关系即可.
解答:
 解:如图:设CD中点为O,作OF⊥AB于F,
解:如图:设CD中点为O,作OF⊥AB于F,∵OF=
 (AD+BC)(梯形中位线定理)
(AD+BC)(梯形中位线定理)又∵CD>AD+BC
∴OF=
 (AD+BC)<
(AD+BC)< CD.
CD.故⊙O与AB相交.
故选C.
点评:本题考查了直线和圆的位置关系,利用中位线定理比较出AB到圆心的距离与半径的关系是解题的关键.

练习册系列答案
相关题目
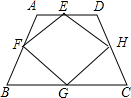 如图,已知等腰梯形ABCD,AD∥BC,AB=DC,E、F、G、H 分别是AD、AB、BC、CD的中点,则四边形EFGH一定是( )
如图,已知等腰梯形ABCD,AD∥BC,AB=DC,E、F、G、H 分别是AD、AB、BC、CD的中点,则四边形EFGH一定是( )| A、正方形 | B、矩形 | C、菱形 | D、等腰梯形 |

 如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.
如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.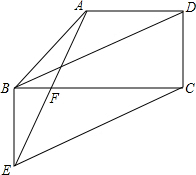 如图,梯形ABCD,AD∥BC,连接BD,过B、C分别作CD、BD的平行线交于E,连接AE交BC于F,求证:F是AE的中点.
如图,梯形ABCD,AD∥BC,连接BD,过B、C分别作CD、BD的平行线交于E,连接AE交BC于F,求证:F是AE的中点.