题目内容
点A的坐标为(
,0),把点A绕着坐标原点顺时针旋转135°到点B,那么点B的坐标是( )
| 2 |
分析:画出图形分析,点B位置如图所示.作BC⊥y轴于C点,根据∠AOB=135°,有∠BOC=45°,然后解直角三角形求OC、BC的长度,根据B点在第三象限确定其坐标.
解答: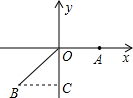 解:点B位置如图所示.
解:点B位置如图所示.
作BC⊥y轴于C点.
∵A(
,0)
∴OA=
.
∵∠AOB=135°,
∴∠BOC=45°.
又∵OB=OA=
,
∴BC=1,OC=1.
因B在第三象限,所以B(-1,-1).
故选C.
 解:点B位置如图所示.
解:点B位置如图所示.作BC⊥y轴于C点.
∵A(
| 2 |
∴OA=
| 2 |
∵∠AOB=135°,
∴∠BOC=45°.
又∵OB=OA=
| 2 |
∴BC=1,OC=1.
因B在第三象限,所以B(-1,-1).
故选C.
点评:本题考查了坐标与图形的变化,画出图形解直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).画出△OAB绕点O逆时针旋转90°后的△OA1B1,并求出AA1的长.
如图所示,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).画出△OAB绕点O逆时针旋转90°后的△OA1B1,并求出AA1的长. 线
线
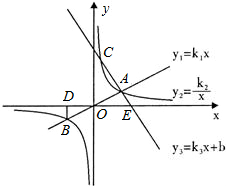 如图,正比例函数y1=k1x与反比例函数y2=
如图,正比例函数y1=k1x与反比例函数y2=