题目内容
如图1,在等腰梯形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() .
.
(1)求点![]() 到
到![]() 的距离;
的距离;
(2)点![]() 为线段
为线段![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() ,连结
,连结![]() ,设
,设![]() .
.
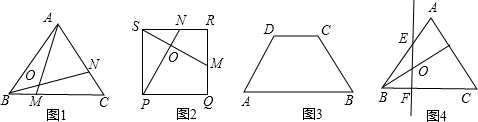
①当点![]() 在线段
在线段![]() 上时(如图2),
上时(如图2),![]() 的形状是否发生改变?若不变,求出
的形状是否发生改变?若不变,求出![]() 的周长;若改变,请说明理由;
的周长;若改变,请说明理由;
②当点![]() 在线段
在线段![]() 上时(如图3),是否存在点
上时(如图3),是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
1)如图1,

过点![]() 作
作![]() 于点
于点![]()
∵![]() 为
为![]() 的中点,
的中点,
∴![]()
在![]() 中,
中,![]() ∴
∴![]()
∴![]()
即点![]() 到
到![]() 的距离为
的距离为![]()
(2)①当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 的形状不发生改变.
的形状不发生改变.
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() ,
,![]()
同理![]()
如图2,
 |
过点![]() 作
作![]() 于
于![]() ,∵
,∵![]()
∴![]()
∴![]()
∴![]()
则![]()
在![]() 中,
中,
∴![]() 的周长=
的周长=![]()
②当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 的形状发生改变,但
的形状发生改变,但![]() 恒为等边三角形.
恒为等边三角形.
当![]() 时,如图3,作
时,如图3,作![]() 于
于![]() ,则
,则![]()
类似①,![]()
∴![]()
∵![]() 是等边三角形,∴
是等边三角形,∴![]()
此时,![]()
 当
当![]() 时,如图4,这时
时,如图4,这时![]()
此时,![]()
当![]() 时,如图5,
时,如图5,![]()
则![]() 又
又![]()
∴![]()
因此点![]() 与
与![]() 重合,
重合,![]() 为直角三角形.
为直角三角形.
∴![]()
此时,![]()
综上所述,当![]() 或4或
或4或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目