Question

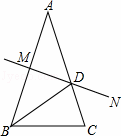
如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ=60°，且BP=BQ，连结CQ．

（1）观察并猜想AP与CQ之间的大小关系，并说明理由．

（2）若PA=3，PB=4，PC=5，连结PQ，判断△PQC的形状并说明理由．

Answer 1

 解：（1）AP=CQ．理由如下：

∵∠PBQ=60°，且BQ=BP，

∴△BPQ为等边三角形，

∵∠ABP+∠CBP=60°，∠CBQ+∠CBP=60°，

∴∠CBQ=∠ABP，

在△ABP和△CBQ中，

，

∴△ABP≌△CBQ（SAS），

∴AP=CQ；

（2）∵等边△ABC和等边△BPQ中，

PB=PQ=4，PA=QC=3，

∵PQ²+CQ²=PC²，

∴△PQC为直角三角形（勾股定理逆定理）．