题目内容
17.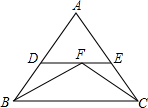 如图,在△ABC中,AB=AC,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,F为DE的中点,求证:DB=EC.
如图,在△ABC中,AB=AC,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,F为DE的中点,求证:DB=EC.
分析 利用角平分线性质可得两组角相等,再结合平行线的性质,可证出∠DBF=∠FBC,∠FBC=∠DFB,根据等角对等边证得DB=DF,同理证得EC=EF,根据F为DE的中点,即可证得结论.
解答 证明:∵DE∥BC,
∴∠FBC=∠DFB,
又∵BF是∠ABC的角平分线,
∴∠DBF=∠FBC,
∴∠DBF=∠DFB,
∴DB=DF,
同理:EC=EF,
∵DF=EF,
∴DB=EC.
点评 本题考查了角平分线性质、平行线性质、以及等角对等边的性质等.熟练掌握这些性质是解题的关键.

练习册系列答案
相关题目
5.到三角形三个顶点的距离相等的点一定是三角形( )的交点.
| A. | 三条角平分线 | B. | 三条边的垂直平分线 | ||
| C. | 三条高 | D. | 三条中线 |
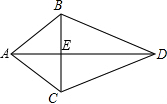 如图,已知AB=AC,BD=CD,AD与BC交于点E.请写出三个不同类型的正确结论.(不添加字母和辅助线,不要求证明)
如图,已知AB=AC,BD=CD,AD与BC交于点E.请写出三个不同类型的正确结论.(不添加字母和辅助线,不要求证明)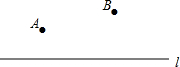 如图,已知直线l及其同侧两点A、B.
如图,已知直线l及其同侧两点A、B. 如图,已知不等边三角形ABC.求作:作一个三角形,使它与△ABC有公共顶点C,并且与△ABC全等(不写作法,保留作图痕迹).
如图,已知不等边三角形ABC.求作:作一个三角形,使它与△ABC有公共顶点C,并且与△ABC全等(不写作法,保留作图痕迹).