题目内容
7.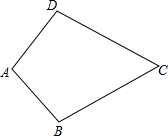 已知,如图:四边形ABCD中,AB=AD,BC=CD.
已知,如图:四边形ABCD中,AB=AD,BC=CD.(1)求证:∠B=∠D;
(2)连接BD,交AC于O点.则AC与BD有怎样的关系?并说明理由.
分析 (1)连接AC,用SSS证明△ABC≌△ADC,即可得到∠B=∠D.
(2)AC⊥BD,利用垂直平分线的性质,即可解答.
解答 解:(1)如图1,连接AC,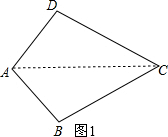
在△ABC和△ADC中,
$\left\{\begin{array}{l}{AD=AB}\\{BC=DC}\\{AC=AC}\end{array}\right.$
∴△ABC≌△ADC,
∴∠B=∠D.
(2)AC⊥BD,
如图2,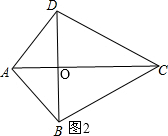
∵AB=AD,
∴点A在线段BD的垂直平分线,
∵BC=CD,
∴点C在线段BD的垂直平分线,
∴AC垂直平分线段BD,
∴AC⊥BD.
点评 本题考查了全等三角形的性质与判定、垂直平分线的性质,解决本题的关键是证明△ABC≌△ADC.

练习册系列答案
相关题目
12.下列计算中正确的有( )
①0-(+3)=+3;②0-(-3)=+3;③+5-5=0;④($-\frac{1}{3}$)-0=$\frac{1}{3}$;⑤$-\frac{1}{2}×(-\frac{2}{3})=\frac{1}{3}$;⑥$-\frac{5}{2}÷2=-5$.
①0-(+3)=+3;②0-(-3)=+3;③+5-5=0;④($-\frac{1}{3}$)-0=$\frac{1}{3}$;⑤$-\frac{1}{2}×(-\frac{2}{3})=\frac{1}{3}$;⑥$-\frac{5}{2}÷2=-5$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.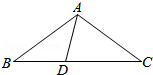 如图,在△ABC中,D是BC上一点,若∠B=∠C=∠BAD,∠DAC=∠ADC,∠BAC的度数为( )
如图,在△ABC中,D是BC上一点,若∠B=∠C=∠BAD,∠DAC=∠ADC,∠BAC的度数为( )
 如图,在△ABC中,D是BC上一点,若∠B=∠C=∠BAD,∠DAC=∠ADC,∠BAC的度数为( )
如图,在△ABC中,D是BC上一点,若∠B=∠C=∠BAD,∠DAC=∠ADC,∠BAC的度数为( )| A. | 36度 | B. | 72度 | C. | 98度 | D. | 108度 |
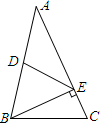 如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为6.
如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为6.