题目内容
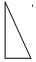
18.若多项式(5-m)x2+(m-2)x+3中不含x的二次项,则m的值是( )| A. | 5 | B. | -5 | C. | 2 | D. | -2 |
分析 根据已知得出方程5-m=0,求出方程的解即可.
解答 解:∵多项式(5-m)x2+(m-2)x+3中不含x的二次项,
∴5-m=0,
∴m=5,
故选A.
点评 本题考查了多项式,能根据题意得出方程是解此题的关键.

练习册系列答案
相关题目
11.线段CD是由线段AB平移得到的,点A(-2,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为( )
| A. | (2,9) | B. | (5,3) | C. | (2,2) | D. | (-9,-4) |
12.下列计算正确的是( )
| A. | 2×32=36 | B. | -0.5÷$\frac{1}{4}$=2 | C. | -3÷$\frac{1}{4}$×4=-3 | D. | (-$\frac{3}{4}$)×(-8)=6 |
8.若等腰三角形的两边满足x2-6x+8=0,则它的周长为( )
| A. | 8或10 | B. | 10或12 | C. | 8 | D. | 10 |
15.下列各式中,去括号后得x-y+z的是( )
| A. | x-(y+z) | B. | -(x-y)+z | C. | x-(y-z) | D. | -(x+y)+z |
3.在△ABC中,若点D、E分别在边AB、AC上,则下列条件中,一定能推出DE∥BC的是( )
| A. | $\frac{ED}{BC}$=$\frac{AD}{AB}$ | B. | $\frac{ED}{BC}$=$\frac{AD}{DB}$ | C. | $\frac{AD}{DB}$=$\frac{EC}{AE}$ | D. | $\frac{AD}{AE}$=$\frac{DB}{EC}$ |
7. 如图,某河堤迎水坡AB的坡比i=1:$\sqrt{3}$,堤高BC=5m,则坡面AB的长是( )
如图,某河堤迎水坡AB的坡比i=1:$\sqrt{3}$,堤高BC=5m,则坡面AB的长是( )
 如图,某河堤迎水坡AB的坡比i=1:$\sqrt{3}$,堤高BC=5m,则坡面AB的长是( )
如图,某河堤迎水坡AB的坡比i=1:$\sqrt{3}$,堤高BC=5m,则坡面AB的长是( )| A. | 5 m | B. | 10m | C. | 15 m | D. | 5 m |
8. 如图,在△ABC中,∠DAC=77°,∠B=58°,则∠ACB=( )
如图,在△ABC中,∠DAC=77°,∠B=58°,则∠ACB=( )
 如图,在△ABC中,∠DAC=77°,∠B=58°,则∠ACB=( )
如图,在△ABC中,∠DAC=77°,∠B=58°,则∠ACB=( )| A. | 21° | B. | 19° | C. | 135° | D. | 以上答案都不对 |
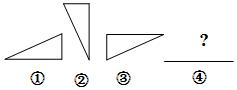 如图,将一个直角三角形按①②③④的顺序依次进行变换,观察图形的变换规律,确定④对应的图形为( )
如图,将一个直角三角形按①②③④的顺序依次进行变换,观察图形的变换规律,确定④对应的图形为( )