题目内容
若△ABC内切圆的切点将该圆圆周分为7:8:9三条弧,则△ABC的最小内角为________.
45°
分析:连接OF、OE、OD,设弧ED:弧EF:弧FD=7:8:9,求出∠EOF=120°,∠EOD=105°,∠FOD=135°,根据⊙O是△ABC的内切圆得出∠AFO=∠AEO=∠CEO=∠CDO=∠BDO=∠BFO=90°,求出∠B的度数即可.
解答: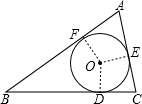
连接OF、OE、OD,设弧ED:弧EF:弧FD=7:8:9,
则∠EOF= ×360°=120°,∠EOD=
×360°=120°,∠EOD=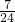 ×360°=105°,∠FOD=
×360°=105°,∠FOD=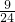 ×360°=135°,
×360°=135°,
∵⊙O是△ABC的内切圆,切点分别为E、D、F,
∴∠AFO=∠AEO=∠CEO=∠CDO=∠BDO=∠BFO=90°,
∴∠FOD对的角B最小,即∠B=180°-135°=45°,
故答案为:45°.
点评:本题考查了三角形的内切圆与内心的应用,关键是求出∠FOD的度数和得出∠B=180°-∠FOD.
分析:连接OF、OE、OD,设弧ED:弧EF:弧FD=7:8:9,求出∠EOF=120°,∠EOD=105°,∠FOD=135°,根据⊙O是△ABC的内切圆得出∠AFO=∠AEO=∠CEO=∠CDO=∠BDO=∠BFO=90°,求出∠B的度数即可.
解答:

连接OF、OE、OD,设弧ED:弧EF:弧FD=7:8:9,
则∠EOF=
 ×360°=120°,∠EOD=
×360°=120°,∠EOD=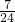 ×360°=105°,∠FOD=
×360°=105°,∠FOD=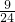 ×360°=135°,
×360°=135°,∵⊙O是△ABC的内切圆,切点分别为E、D、F,
∴∠AFO=∠AEO=∠CEO=∠CDO=∠BDO=∠BFO=90°,
∴∠FOD对的角B最小,即∠B=180°-135°=45°,
故答案为:45°.
点评:本题考查了三角形的内切圆与内心的应用,关键是求出∠FOD的度数和得出∠B=180°-∠FOD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,若等边△ABC的边长为2
如图,若等边△ABC的边长为2| 3 |
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
 如图,△ABC的内切圆分别切
如图,△ABC的内切圆分别切
 (2007•西城区二模)若等边△ABC的边长为6cm长,内切圆O分别切三边于D、E、F,则阴影部分的面积是( )
(2007•西城区二模)若等边△ABC的边长为6cm长,内切圆O分别切三边于D、E、F,则阴影部分的面积是( )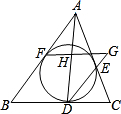 如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.
如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.