题目内容
 如图,∠ABC=31°,又∠BAC的平分线与∠FCB的平分线CE相交于E点,则∠AEC为
如图,∠ABC=31°,又∠BAC的平分线与∠FCB的平分线CE相交于E点,则∠AEC为
- A.14.5°
- B.15.5°
- C.16.5°
- D.20°
B
分析:设∠BAC=2x°,根据三角形外角的性质得:∠BCE=(x+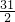 )°,然后根据AE平分∠BAC和外角的性质得∠E+x=x+
)°,然后根据AE平分∠BAC和外角的性质得∠E+x=x+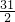 ,解得:∠E=15.5°.
,解得:∠E=15.5°.
解答:设∠BAC=2x,
则根据三角形外角的性质得:∠BCF=2x+31°,
∵∠BAC的平分线与∠FCB的平分线CE相交于E点,
∴∠EAC=x,∠ECD=∠E+x,
∵∠ECD是△AEC的外角,
∴∠ECD=∠E+∠EAD,
即:∠E+x=x+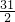 ,
,
解得:∠E=15.5°.
故选B.
点评:本题综合考查了三角形的内角和定理及三角形的外角的性质,解题时设出了一个中介值,从而使运算方便.
分析:设∠BAC=2x°,根据三角形外角的性质得:∠BCE=(x+
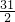 )°,然后根据AE平分∠BAC和外角的性质得∠E+x=x+
)°,然后根据AE平分∠BAC和外角的性质得∠E+x=x+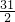 ,解得:∠E=15.5°.
,解得:∠E=15.5°.解答:设∠BAC=2x,
则根据三角形外角的性质得:∠BCF=2x+31°,
∵∠BAC的平分线与∠FCB的平分线CE相交于E点,
∴∠EAC=x,∠ECD=∠E+x,
∵∠ECD是△AEC的外角,
∴∠ECD=∠E+∠EAD,
即:∠E+x=x+
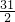 ,
,解得:∠E=15.5°.
故选B.
点评:本题综合考查了三角形的内角和定理及三角形的外角的性质,解题时设出了一个中介值,从而使运算方便.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,∠ABC=31°,又∠BAC的平分线与∠FCB的平分线CE相交于E点,则∠AEC为( )
如图,∠ABC=31°,又∠BAC的平分线与∠FCB的平分线CE相交于E点,则∠AEC为( )| A、14.5° | B、15.5° | C、16.5° | D、20° |
 如图,△ABC和△A1B1C1均为等边三角形,点O既是AC的中点,又是A1C1的中点,则AA1:BB1=
如图,△ABC和△A1B1C1均为等边三角形,点O既是AC的中点,又是A1C1的中点,则AA1:BB1=
