题目内容
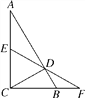
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是AC的中点,ED的延长线与CB的延长线交于点F.
(1)若FD=2FB,求![]() 的值;
的值;
(2)若AC=2![]() ,BC=
,BC=![]() ,求S△FDC的值.
,求S△FDC的值.

【答案】(1)![]() ; (2)4.
; (2)4.
【解析】试题分析:
(1)由已知中∠ACB=90°,CD⊥AB,点E为AC中点,易证∠A=∠BCD,DE=AE,由此可得∠BCD=∠A=∠ADE=∠BDF,再结合∠F=∠F可证△BDF∽△DCF,就可得![]() ;
;
(2)由已知易证△BDC∽△BCA,AB=![]() ,由此可得BD∶CD=BC∶AC=
,由此可得BD∶CD=BC∶AC=![]() ,
,![]() ,这样由S△ABC=
,这样由S△ABC=![]() AC
AC![]() BC=
BC=![]() 可得S△BDC=3;
可得S△BDC=3;
再由△BDF∽△DCF可得![]() ,∴
,∴![]() ,∴S△FDC=4.
,∴S△FDC=4.
试题解析:
解:(1)∵∠ACB=90°,CD⊥AB,
∴∠A+∠ABC=∠DCB+∠ABC=90°,
∴∠A=∠DCB.
∵E是AC的中点,∠ADC=90°,
∴ED=EA,
∴∠A=∠EDA.
∵∠BDF=∠EDA,
∴∠DCB=∠BDF.
又∵∠F=∠F,
∴△BDF∽△DCF,
∴![]() .
.
(2)∵∠ACB=90°,CD⊥AB,
∴∠BDC=∠ACB=90°.
∵∠ABC=∠CBD,
∴△BDC∽△BCA,
∴BD∶CD=BC∶AC=![]() .
.
∵在Rt△BAC中,由勾股定理可得AB=![]() ,
,
∴![]() .
.
又∵S△ABC=![]() AC
AC![]() BC=
BC=![]() ,
,
∴S△BDC=![]() .
.
∵△BDF∽△DCF,
∴![]() ,
,
∴![]() .
.
∴S△DCF=4.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目