Question

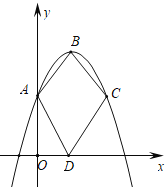
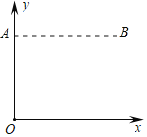
【题目】某一房间内A、B两点之间设有探测报警装置，小车（不计大小）在房间内运动，当小车从AB之间（不包括A、B两点）经过时，将触发报警．现将A、B两点放置于平面直角坐标系中，（如图），已知点A、B的坐标分别为（0，4），（4，4），小车沿抛物线（＜0）运动．若小车在运动过程中触发两次报警装置，则的取值范围是__________．

Answer 1

【答案】＜＜

【解析】

先把抛物线解析式分解因式，得其与x轴的交点坐标及对称轴，再分别代入临界点的坐标（0，4）和（4，4），结合二次项系数大小与开口大小及与x轴的交点为定点等即可解答．

解：抛物线，
∴其对称轴为：，且图象与x轴交于（，0），（3，0）．
∵抛物线顶点为（1，），当顶点在线段AB上时，有，则；
当抛物线过点（0，4）时，代入解析式得：；
∴，

由对称轴为x=1及图象与x轴交于（，0），（3，0）可知，

当＜＜时，抛物线与线段AB有两个交点；

∴小车在运动过程中触发两次报警装置，则的取值范围是＜＜；

故答案为：＜＜.