题目内容
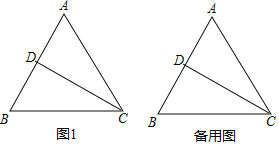
【题目】如图1,在等边三角形![]() 中,
中,![]() 为中线,点
为中线,点![]() 在线段
在线段![]() 上运动,将线段
上运动,将线段![]() 绕点
绕点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 的对应点
的对应点![]() 落在射线
落在射线![]() 上,连接
上,连接![]() ,设
,设![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,
时,
①在图1中依题意画出图形,并求![]() (用含
(用含![]() 的式子表示);
的式子表示);
②探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(2)当![]() 时,直接写出线段
时,直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]()
【解析】
(1)①先根据等边三角形的性质的![]() ,进而得出
,进而得出![]() ,最后用三角形的内角和定理即可得出结论;②先判断出
,最后用三角形的内角和定理即可得出结论;②先判断出![]() ,得出
,得出![]() ,再判断出
,再判断出![]() 是底角为30度的等腰三角形,再构造出直角三角形即可得出结论;(2)同②的方法即可得出结论.
是底角为30度的等腰三角形,再构造出直角三角形即可得出结论;(2)同②的方法即可得出结论.
(1)当![]() 时,
时,
①画出的图形如图1所示,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵![]() 为等边三角形的中线
为等边三角形的中线
∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∵![]() 为线段
为线段![]() 上的点,
上的点,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∵线段![]() 为线段
为线段![]() 绕点
绕点![]() 顺时针旋转所得,
顺时针旋转所得,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]()
![]() ;
;
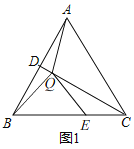
②![]() ;
;
如图2,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() .
.
∵![]() ,点
,点![]() 在
在![]() 上,
上,
∴![]()
![]() .
.
∵点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
∵在等边三角形![]() 中,
中,![]() 为中线,点
为中线,点![]() 在
在![]() 上,
上,
∴![]() ,
,
即![]() 为底角为
为底角为![]() 的等腰三角形.
的等腰三角形.
∴![]() .
.
∴![]() .
.
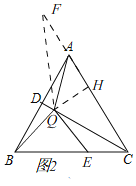
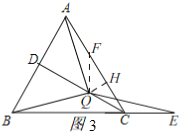
(2)如图3,当![]() 时,
时,
在![]() 上取一点
上取一点![]() 使
使![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵![]() 为等边三角形的中线,
为等边三角形的中线,
∵![]() 为线段
为线段![]() 上的点,
上的点,
∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∵线段![]() 为线段
为线段![]() 绕点
绕点![]() 顺时针旋转所得,
顺时针旋转所得,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
∵在等边三角形![]() 中,
中,![]() 为中线,点
为中线,点![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]() .
.
∴![]() .
.

 提分百分百检测卷系列答案
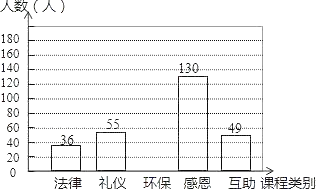
提分百分百检测卷系列答案【题目】某校有学生3600人,在“文明我先行”的活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了一些学生,并制成统计表和统计图:
课程类别 | 频数 | 频率 |
法律 | 36 | 0.09 |
礼仪 | 55 | 0.1375 |
环保 | m | a |
感恩 | 130 | 0.325 |
互助 | 49 | 0.1225 |
合计 | n | 1.00 |
(1)在这次调查活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”)a= ,m= ,n= .
(2)请补全条形统计图,如果要画一个“校本课程报名意向扇形统计图”,那么“环保”类校本课程所对应的扇形圆心角应为 度;
(3)请估算该校3600名学生中选择“感恩”校本课程的学生约有多少人?
【题目】北京世界园艺博览会(简称“世园会”)园区4月29日正式开园,门票价格如下:
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上在线上购买世园会门票,票价可打九折,但仅限于普通票.
某大家庭计划在6月1日集体入园参观游览,通过计算发现:若提前两天线上购票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有______人.