题目内容
已知方程组 的两个解为
的两个解为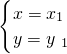 和
和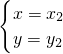 ,且x1,x2是两个不相等的实数,若x12+x22-3x1x2=8a2-6a-11.
,且x1,x2是两个不相等的实数,若x12+x22-3x1x2=8a2-6a-11.
(1)求a的值;
(2)不解方程组判断方程组的两个解能否都是正数?为什么?
解:(1)由方程组 可得x2-x+a+1=0,
可得x2-x+a+1=0,
由题意知:△=1-4(a+1)=-3-4a>0,
所以a<- .
.
又x1+x2=1,x1x2=a+1,
所以x12+x22-3x1x2=(x1+x2)2-5x1x2=1-5(a+1)=-4-5a=8a2-6a-11,
解得:a=- 或1.又a<-
或1.又a<- ,
,
所以a的值为- .
.
(2)能.
∵x1+x2=1>0,x1x2=a+1= >0,
>0,
∴x1>0,x2>0,且y1=x1+1>0,y2=x2+1>0,
故存在方程组的两个解都为正数.
即可以不解方程组判断方程组的两个解都是正数.
分析:(1)首先将方程(2)代入(1),变成一个关于x的一元二次方程,根据根与系数的关系进行求解;
(2)根据根与系数的关系知道两根之和大于0,两根之积大于0,可以得到结果.
点评:本题主要考查了根与系数的关系和用公式法解一元二次方程,题目很有新意,要好好理解.
 可得x2-x+a+1=0,
可得x2-x+a+1=0,由题意知:△=1-4(a+1)=-3-4a>0,
所以a<-
 .
.又x1+x2=1,x1x2=a+1,
所以x12+x22-3x1x2=(x1+x2)2-5x1x2=1-5(a+1)=-4-5a=8a2-6a-11,
解得:a=-
 或1.又a<-
或1.又a<- ,
,所以a的值为-
 .
.(2)能.
∵x1+x2=1>0,x1x2=a+1=
 >0,
>0,∴x1>0,x2>0,且y1=x1+1>0,y2=x2+1>0,
故存在方程组的两个解都为正数.
即可以不解方程组判断方程组的两个解都是正数.
分析:(1)首先将方程(2)代入(1),变成一个关于x的一元二次方程,根据根与系数的关系进行求解;
(2)根据根与系数的关系知道两根之和大于0,两根之积大于0,可以得到结果.
点评:本题主要考查了根与系数的关系和用公式法解一元二次方程,题目很有新意,要好好理解.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 的两个解为
的两个解为 和
和 ,且
,且 的两个解为
的两个解为 和
和 ,且x1,x2是两个不相等的实数,若x12+x22-3x1x2=8a2-6a-11.
,且x1,x2是两个不相等的实数,若x12+x22-3x1x2=8a2-6a-11.