Question

【题目】如图，在等腰直角中，，D是线段上一点（），连接，过点C作的垂线，交的延长线于点E，交的延长线于点F.

（1）依题意补全图形；

（2）若，求的大小（用含的式子表示）；

（3）若点G在线段上，，连接.

①判断与的位置关系并证明；

②用等式表示之间的数量关系.

Answer 1

【答案】（1）补全图形，如图见解析；（2）；（3）①DG与BC的位置关系: DG⊥BC. 见解析；②2CG2=DG2+AB2.

【解析】

根据题意画出图形解答即可；
根据等腰直角三角形的性质进行解答即可；
根据全等三角形的判定和性质以及垂直的判定解答即可；如图：构造等腰Rt△BPD得PD2=2BD2．利用三角形全等证明△PGD为直角三角形，PG=AB即可得到结论.

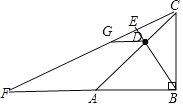
解：补全图形，如图所示：

，，
，
，
，
交BD的延长线于点E，
，
，
，
；
与BC的位置关系：，
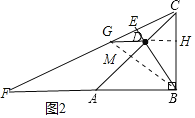
证明如下：
连接BG交AC于点M，延长GD交BC于点H，如图2，

，，，
≌，
，
，
，，
，
，
，
，
；

②如图：作等腰Rt△BPD，连接PG、PD，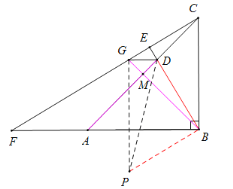

由①得BG⊥AC，∠PBD=90°，

∴∠ADB+∠DBM=90°，∠DBM+∠GBP=90°，

∴∠ADB=∠GBP，

在△ADB和△GBP中，

,

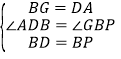∴△ADB≌△GBP（SAS），

∴AB=PG，∠PGB=∠DAB=45°，

由①得，

∴∠PGB+∠MGD=90°，即△PGD为直角三角形，

∴PD2+DG2=PD2

∵PD2=2BD2,BD=CG

∴