题目内容
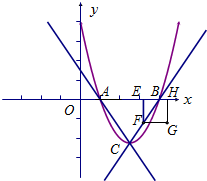 如图,二次函数y=x2-5x+4的图象与x轴交于A,B两点(点A在点B左侧),顶点为C,有一个动点E从点B出发以每秒一个单位向点A运动,过E 作y轴的平行线,交△ABC的边BC或AC于点F,以EF为边在EF右侧作正方形EFGH,设正方形EFGH与△ABC重叠部分面积为S,E点运动时间为t秒.
如图,二次函数y=x2-5x+4的图象与x轴交于A,B两点(点A在点B左侧),顶点为C,有一个动点E从点B出发以每秒一个单位向点A运动,过E 作y轴的平行线,交△ABC的边BC或AC于点F,以EF为边在EF右侧作正方形EFGH,设正方形EFGH与△ABC重叠部分面积为S,E点运动时间为t秒.
(1)求顶点C的坐标和直线AC的解析式;
(2)求当点F在AC边上,G在BC边上时t的值;
(3)求动点E从点B向点A运动过程中,S关于t的函数关系.
(1)解:
∵y=x2-5x+4=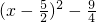 ,
,
顶点C的坐标为(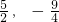 ),
),
∵y=x2-5x+4=(x-1)(x-4),
∴点A(1,0),B(4,0),
设AC直线为y=kx+b,得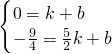 ,
,
解得:k=- ,b=
,b= ,
,
∴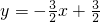 ,
,
答:顶点C的坐标为(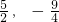 ),直线AC的解析式是
),直线AC的解析式是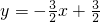 .
.
(2)解:设直线BC的解析式是y=ax+c,
把B(4,0),C( ,-
,- )代入得:0=4a+c且-
)代入得:0=4a+c且- =
= a+c,
a+c,
解得:a= ,c=-6,
,c=-6,
直线BC的解析式为 ,
,
当F在AC边上,G在BC边上时,
点E坐标为(4-t,0),点F坐标为(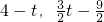 ),
),
得EF=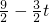 ,
,
而EF=FG,
∵抛物线的对称轴和等腰△ABC的对称轴重合,
∴FG= ,
,
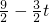 =2t-3,
=2t-3,
∴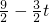 =2t-3,
=2t-3,
解得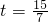 ,
,

答:当点F在AC边上,G在BC边上时t的值是 .
.
(3)解:点E坐标为(4-t,0)随着正方形的移动,重叠部分的形状不同,可分以下几种情况:
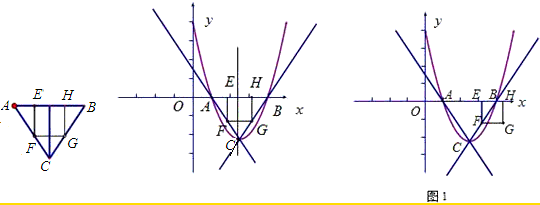
①点F在BC上时,如图1重叠部分是△BEF,
此时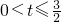 时,点F坐标为(
时,点F坐标为(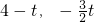 ),
),
 =
=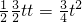 ,
,
②点F在AC上时,点F坐标为(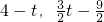 )又可分三种情况:
)又可分三种情况:
Ⅰ.如图2,EB≤EH时重叠部分是直角梯形EFKB(设FG与直线BC交于点K),
此时 <t≤
<t≤ ,
,
∴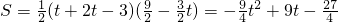 ,
,
Ⅱ.如图3,EB>EH,点G在BC下方时,重叠部分是五边形EFKMH(设FG与直线BC交于点K,GH与直线BC交于点M),
此时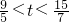 ,
,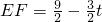 ,
,
点H坐标为(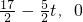 ),点M坐标为(
),点M坐标为(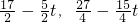 ),
),
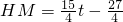 ,
,
 ,
,
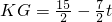 ,
,
∴S=SEFGH-S△KMG=(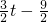 )2
)2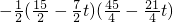 ,
,
=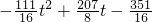 ,
,
Ⅲ.如图4,点G在BC上或BC上方时,重叠部分是正方形EFGH,此时 ≤t<3,
≤t<3,
∴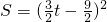 =
= t2-
t2- t+
t+ ,
,
答:动点E从点B向点A运动过程中,S关于t的函数关系S= t2(0<t≤
t2(0<t≤ )或S=-
)或S=- t2+9t-
t2+9t- (
( <t≤
<t≤ )或S=-
)或S=-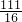 t2+
t2+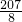 t-
t-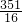 (
( <t<
<t< )或S=
)或S= t2-
t2- t+
t+ (
( ≤t<3).
≤t<3).
分析:(1)把y=x2-5x+4化成顶点式,求出顶点C的坐标,y=x2-5x+4化成(x-1)(x-4),求出A、B的坐标,设AC直线为y=kx+b,把A、C的坐标代入就能求出直线AC的解析式;
(2)设直线BC的解析式是y=ax+c,把B、C的坐标代入就能求出直线BC,点E坐标为(4-t,0),点F坐标为(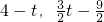 ),求出EF=
),求出EF=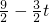 ,FG=2t-3,根据EF=FG,即可求出t的值;
,FG=2t-3,根据EF=FG,即可求出t的值;
(3)可分以下几种情况:①点F在BC上时,如图1重叠部分是△BEF2,此时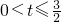 时,点F坐标为(
时,点F坐标为(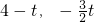 ),根据三角形的面积公式即可求出;②I如图2,EB≤EH时重叠部分是直角梯形EFKB,此时
),根据三角形的面积公式即可求出;②I如图2,EB≤EH时重叠部分是直角梯形EFKB,此时 <t≤
<t≤ ,根据三角形的面积公式即可求出;II如图3,EB>EH,点G在BC下方时,重叠部分是五边形EFKMH,此时
,根据三角形的面积公式即可求出;II如图3,EB>EH,点G在BC下方时,重叠部分是五边形EFKMH,此时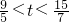 ,
,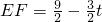 ,因为S=S正方形EFGH-S△KMG,根据三角形的面积公式即可求出;Ⅲ.如图4,点G在BC上或BC上方时,重叠部分是正方形EFGH,此时
,因为S=S正方形EFGH-S△KMG,根据三角形的面积公式即可求出;Ⅲ.如图4,点G在BC上或BC上方时,重叠部分是正方形EFGH,此时 ≤t<3,
≤t<3,
根据正方形的面积公式求出即可.
点评:本题主要考查对二次函数与X轴的交点,用待定系数法求一次函数的解析式,解二元一次方程组,三角形的面积,用十字相乘法分解因式,二次函数图象上点的坐标特征等知识点的理解和掌握,此题是一个拔高的题目,有一定的难度,用的数学思想是分类讨论思想.

∵y=x2-5x+4=
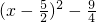 ,
,顶点C的坐标为(
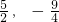 ),
),∵y=x2-5x+4=(x-1)(x-4),
∴点A(1,0),B(4,0),
设AC直线为y=kx+b,得
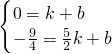 ,
,解得:k=-
 ,b=
,b= ,
,∴
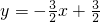 ,
,答:顶点C的坐标为(
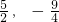 ),直线AC的解析式是
),直线AC的解析式是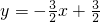 .
.(2)解:设直线BC的解析式是y=ax+c,
把B(4,0),C(
 ,-
,- )代入得:0=4a+c且-
)代入得:0=4a+c且- =
= a+c,
a+c,解得:a=
 ,c=-6,
,c=-6,直线BC的解析式为
 ,
,当F在AC边上,G在BC边上时,
点E坐标为(4-t,0),点F坐标为(
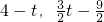 ),
),得EF=
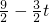 ,
,而EF=FG,
∵抛物线的对称轴和等腰△ABC的对称轴重合,
∴FG=
 ,
,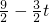 =2t-3,
=2t-3,∴
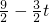 =2t-3,
=2t-3,解得
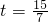 ,
,
答:当点F在AC边上,G在BC边上时t的值是
 .
.(3)解:点E坐标为(4-t,0)随着正方形的移动,重叠部分的形状不同,可分以下几种情况:
①点F在BC上时,如图1重叠部分是△BEF,
此时
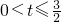 时,点F坐标为(
时,点F坐标为(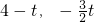 ),
), =
=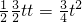 ,
,②点F在AC上时,点F坐标为(
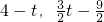 )又可分三种情况:
)又可分三种情况:Ⅰ.如图2,EB≤EH时重叠部分是直角梯形EFKB(设FG与直线BC交于点K),
此时
 <t≤
<t≤ ,
,∴
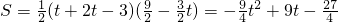 ,
,Ⅱ.如图3,EB>EH,点G在BC下方时,重叠部分是五边形EFKMH(设FG与直线BC交于点K,GH与直线BC交于点M),
此时
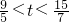 ,
,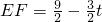 ,
,点H坐标为(
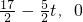 ),点M坐标为(
),点M坐标为(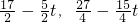 ),
),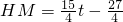 ,
, ,
,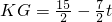 ,
,∴S=SEFGH-S△KMG=(
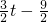 )2
)2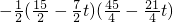 ,
,=
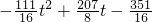 ,
,Ⅲ.如图4,点G在BC上或BC上方时,重叠部分是正方形EFGH,此时
 ≤t<3,
≤t<3,∴
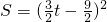 =
= t2-
t2- t+
t+ ,
,答:动点E从点B向点A运动过程中,S关于t的函数关系S=
 t2(0<t≤
t2(0<t≤ )或S=-
)或S=- t2+9t-
t2+9t- (
( <t≤
<t≤ )或S=-
)或S=-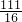 t2+
t2+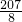 t-
t-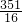 (
( <t<
<t< )或S=
)或S= t2-
t2- t+
t+ (
( ≤t<3).
≤t<3).分析:(1)把y=x2-5x+4化成顶点式,求出顶点C的坐标,y=x2-5x+4化成(x-1)(x-4),求出A、B的坐标,设AC直线为y=kx+b,把A、C的坐标代入就能求出直线AC的解析式;
(2)设直线BC的解析式是y=ax+c,把B、C的坐标代入就能求出直线BC,点E坐标为(4-t,0),点F坐标为(
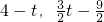 ),求出EF=
),求出EF=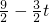 ,FG=2t-3,根据EF=FG,即可求出t的值;
,FG=2t-3,根据EF=FG,即可求出t的值;(3)可分以下几种情况:①点F在BC上时,如图1重叠部分是△BEF2,此时
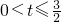 时,点F坐标为(
时,点F坐标为(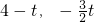 ),根据三角形的面积公式即可求出;②I如图2,EB≤EH时重叠部分是直角梯形EFKB,此时
),根据三角形的面积公式即可求出;②I如图2,EB≤EH时重叠部分是直角梯形EFKB,此时 <t≤
<t≤ ,根据三角形的面积公式即可求出;II如图3,EB>EH,点G在BC下方时,重叠部分是五边形EFKMH,此时
,根据三角形的面积公式即可求出;II如图3,EB>EH,点G在BC下方时,重叠部分是五边形EFKMH,此时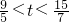 ,
,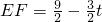 ,因为S=S正方形EFGH-S△KMG,根据三角形的面积公式即可求出;Ⅲ.如图4,点G在BC上或BC上方时,重叠部分是正方形EFGH,此时
,因为S=S正方形EFGH-S△KMG,根据三角形的面积公式即可求出;Ⅲ.如图4,点G在BC上或BC上方时,重叠部分是正方形EFGH,此时 ≤t<3,
≤t<3,根据正方形的面积公式求出即可.
点评:本题主要考查对二次函数与X轴的交点,用待定系数法求一次函数的解析式,解二元一次方程组,三角形的面积,用十字相乘法分解因式,二次函数图象上点的坐标特征等知识点的理解和掌握,此题是一个拔高的题目,有一定的难度,用的数学思想是分类讨论思想.

练习册系列答案
相关题目
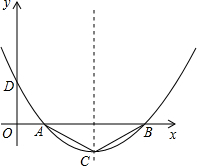 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b