Question

【题目】 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图）就是一例．这个三角形给出了（a+b）n（n=1，2，3，4，5，6）的展开式的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b3展开式中各项的系数，等等．

有如下四个结论：

①（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5；

②当a=-2，b=1时，代数式a3+3a2b+3ab2+b3的值是-1；

③当代数式a4+4a3b+6a2b2+4ab3+b4的值是0时，一定是a=-1，b=1；

④（a+b）n的展开式中的各项系数之和为2n．

上述结论中，正确的有______（写出序号即可）．

Answer 1

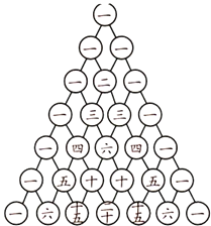
【答案】①②

【解析】

根据题中举例说明，明确杨辉三角的与的展开式的系数间的对应关系，据此逐项分析．

解：∵在杨辉三角形中第三行的三个数1，2，1，恰好对应展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着展开式中各项的系数，等等

∴在杨辉三角形中第行的个数，对应展开式中各项的系数，

①∵展开式中各项的系数，为杨辉三角形中第6行的6个数，

∴；

②∵各项系数对应杨辉三角中的第4行的4个数，

∴，

当时，代数式=；

③∵各项系数对应杨辉三角中的第5行的5个数，

∴，

当代数式时，，不一定是；

④∵当时，展开式各项之和便是系数之和，

∴的展开式中的各项系数之和为，

故答案为：①②．