题目内容
若双曲线y=
过两点(-1,y1),(-3,y2),则y1与y2的大小关系为( )
| 2 |
| x |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、y1与y2大小无法确定 |
考点:反比例函数图象上点的坐标特征
专题:
分析:根据反比例函数图象上点的坐标图特征得到-1•y1=2,-3•y2=2,然后计算出y1和y2比较大小.
解答:解:∵双曲线y=
过两点(-1,y1),(-3,y2),
∴-1•y1=2,-3•y2=2,
∴y1=-2,y2=-
,
∴y1<y2.
故选B.
| 2 |
| x |
∴-1•y1=2,-3•y2=2,
∴y1=-2,y2=-
| 2 |
| 3 |
∴y1<y2.
故选B.
点评:本题考查了反比例函数图象上点的坐标图特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等腰三角形的一个底角为75°,则其顶角为( )
| A、36° | B、30° |
| C、60° | D、75° |
计算(-1)2+(
)-1-5÷(2004-π)0的结果为( )
| 1 |
| 2 |
| A、-2 | ||
B、-
| ||
| C、1 | ||
| D、2 |
某开发公司今年一月份收益达50万元,且一月份、二月份、三月份的收益共为175万元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,根据题意可列方程( )
| A、50(1+x)2=175 |
| B、50+50(1+x)2=175 |
| C、50(1+x)+50(1+x)2=175 |
| D、50+50(1+x)+50(1+x)2=175 |
已知y=1-
,z=1-
,则用含x的代数式表示y为( )
| 1 |
| z |
| 1 |
| x |
A、y=
| ||
B、x=
| ||
C、y=
| ||
D、x=
|
ABC中,AB=AC=4,BC=a,则a的取值范围是( )
| A、a>0 | B、0<a<4 |
| C、4<a<8 | D、0<a<8 |
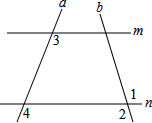 如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空).
如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空).