题目内容
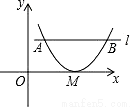
如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c与x轴只有一个交点M，与平行于x轴的直线l交于A、B两点，若AB=3，则点M到直线l的距离为（ ）
A. 
B. 
C. 2 D. 
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
全优冲刺100分系列答案英才点津系列答案红果子三级测试卷系列答案题目内容
如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c与x轴只有一个交点M，与平行于x轴的直线l交于A、B两点，若AB=3，则点M到直线l的距离为（ ）
A. B. C. 2 D.
全优冲刺100分系列答案英才点津系列答案红果子三级测试卷系列答案
B. 
C. 
D. 
