Question

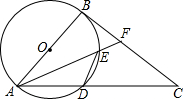如图，以Rt△ABC的边AB为直径的⊙O交斜边AC于点D，点F为BC上一点，AF交⊙O于点E，且∠C=∠BAF．
（1）求证：DE∥AB；
（2）若⊙O的半径为5，AE=2AD，求DE的长．

Answer 1

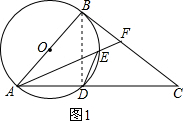（1）证明：如图1，连DB，
∵AB为直径，
∴DB⊥AC，
∵△ABC为直角三角形，
∴∠C=∠ABD=∠DEA，
又∵∠C=∠BAF，
∴∠BAF=∠DEA，
∴DE∥AB；

（2）解：连BE，
∵DE∥AB，
∴∠BAE=∠AED，
∴AD=BE，
在Rt△ABD与Rt△BAE中，
∵，
∴Rt△ABD≌Rt△BAE（HL），
∴BD=AE=2AD，
设AD=x，则BD=2x，
在Rt△ABD中，x²+（2x）²=10²，
∴AD=2，BD=4
过D作DM⊥AB，过O作ON⊥ED，
∴AD•BD=AB•DM，
∴DM===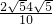4=ON，
连OD，在Rt△OND中，
∵DN=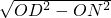==3，
∴ED=2DN=6．
分析：（1）连DB，根据AB为直径可知DB⊥AC，由于△ABC为直角三角形，所以∠C=∠ABD=∠DEA，再根据∠C=∠BAF可知∠BAF=∠DEA，故可得出结论；
（2）连BE，由（1）知DE∥AB，故可得出AD=BE，由全等三角形的判定定理得出Rt△ABD≌Rt△BAE，所以BD=AE=2AD，设AD=x，则BD=2x，在Rt△ABD中根据勾股定理可求出AD，BD的长，过D作DM⊥AB，过O作ON⊥ED，由AD•BD=AB•DM可得出DM的长，连OD，在Rt△OND中，由勾股定理可求出DN的长，由ED=2DN即可得出结论．
点评：本题考查的是圆周角角定理，即在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．