题目内容
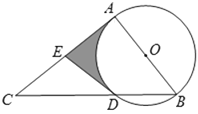
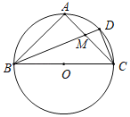
【题目】如图,在⊙O中,BC为直径,A为弧BC的中点,点D在弧AC上,BD与AC相交于M,若CD=1,BC=![]() ,则DM的长是( )
,则DM的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由已知条件易知![]() 为等腰直角三角形,∠BDC=90°,进而可得AB=AC=
为等腰直角三角形,∠BDC=90°,进而可得AB=AC=![]() ,BD=3,由∠BAC=∠BDC=90°,∠AMB=∠DMC可得
,BD=3,由∠BAC=∠BDC=90°,∠AMB=∠DMC可得![]() ,进而可得比例式
,进而可得比例式![]() ,设DM的边长为x进而可以用x表示出其他线段长度,代入比例式解出即为DM的边长.
,设DM的边长为x进而可以用x表示出其他线段长度,代入比例式解出即为DM的边长.
∵BC为直径,
∴∠BAC=∠BDC=90°,
∵A为弧BC的中点,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∵CD=1,BC=![]() ,
,
∴AB=AC=![]() ,BD=3,
,BD=3,
∵∠BAC=∠BDC=90°,∠AMB=∠DMC,
∴![]() ,
,
∴![]() ,
,
∵AB=![]() ,CD=1,
,CD=1,
∴![]() ,
,
设DM=x,则AM=![]() x,则BM=3-x,CM=
x,则BM=3-x,CM=![]() ,
,
∴![]() ,
,
解得:![]() ,
,
即DM=![]() ,
,
故答案为:D.

练习册系列答案
相关题目