题目内容
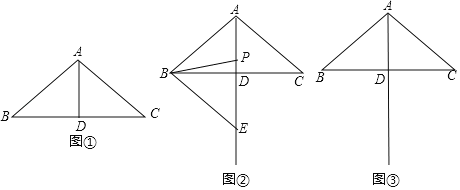
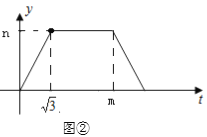
【题目】如图,在平行四边形ABCD中,∠D=60°,点M在线段AD上,DM= ![]() ,AM=2,点E从点D出发,沿着D-C-B-A匀速运动,速度为每秒2个单位长度,达到A点后停止运动,设△MDE的面积为y,点E运动的时间为t(s),y与t的部分函数关系如图②所示.
,AM=2,点E从点D出发,沿着D-C-B-A匀速运动,速度为每秒2个单位长度,达到A点后停止运动,设△MDE的面积为y,点E运动的时间为t(s),y与t的部分函数关系如图②所示.
(1)如图①中,DC=_____,如图②中,m=_______,n=_____.
(2)在E点运动过程中,将平行四边形沿ME所在直线折叠,则t为何值时,折叠后顶点D的对应点D′落在平行四边形的一边上.

【答案】(1)![]() ;
;![]() +1;
+1;![]() ;(2)t=
;(2)t=![]() 或
或![]() 或
或![]() -3
-3
【解析】
(1)先根据题意判断出![]() 时表示的是点E到达点C处,再根据“时间×速度=距离”得出DC即可;
时表示的是点E到达点C处,再根据“时间×速度=距离”得出DC即可;![]() 表示的是点E运动到点B的运动时间;点E从点C到点B过程中y的值是不变的,
表示的是点E运动到点B的运动时间;点E从点C到点B过程中y的值是不变的,![]() 表示的就是点E从点C到点B时y的值,过点C做CF⊥AD垂足为F,再根据三角形面积公式求解即可;
表示的就是点E从点C到点B时y的值,过点C做CF⊥AD垂足为F,再根据三角形面积公式求解即可;
(2)要分三种情况讨论,第一种:当D′与C重合,E为CD的中点;第二种:当D′在BC上,E与C重合;第三种:当D′在AB上时,过点D′作DA延长线的垂线,使![]() 垂足为F,
垂足为F,![]() 垂足为G,过点D作BC延长线的垂线,使
垂足为G,过点D作BC延长线的垂线,使![]() 垂足为H,连接D′E和DE,设
垂足为H,连接D′E和DE,设![]() ,在
,在![]() 中根据勾股定理列出方程
中根据勾股定理列出方程![]() ,再
,再![]() ,然后根据在
,然后根据在![]() 和
和![]() 中
中![]() ,利用双勾股定理
,利用双勾股定理![]() 列出方程求解即可.
列出方程求解即可.
(1)由题意可知:点E从点C到点B过程中y的值是不变的,
∴![]() 时点E到达点C处,
时点E到达点C处,![]() 时点E到达点B处
时点E到达点B处
∴点E从点D到点C的运动时间为![]()
∴![]()
∵平行四边形ABCD
∴![]()
∴点E从点C到点B的运动时间为:![]()
∴![]()
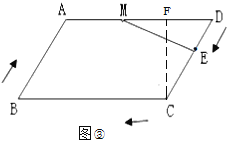
过点C做CF⊥AD垂足为F,如图③所示:
∵∠D=60°
∴![]()
∵点E从点C到点B过程中y的值是不变的
∴![]()
(2)第一种情况:如图④所示:
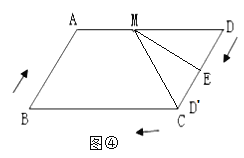
当D′与C重合,E为CD的中点,
∴![]()
∴此时![]()
第二种情况:如图⑤所示:
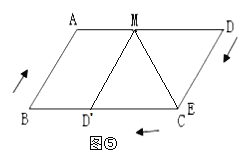
当D′在BC上,E与C重合,
∴此时![]()
第三种情况:如图⑥所示:
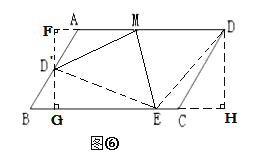
当D′在AB上时,过点D′作DA延长线的垂线,使![]() 垂足为F,
垂足为F,![]() 垂足为G,过点D作BC延长线的垂线,使
垂足为G,过点D作BC延长线的垂线,使![]() 垂足为H,连接D′E和DE,
垂足为H,连接D′E和DE,
∵平行四边形ABCD中,∠D=60°, ![]()
∴∠B=60°,![]()
∴![]()
设![]() ,则
,则![]()
∴![]()
∴![]()
解得:![]() 或
或![]() (舍去)
(舍去)
∴![]()
∴![]()
由(1)中可知![]()
∴![]()
∴![]()
∵![]()
∴![]()
设![]() ,则
,则![]()
∴![]()
根据翻折原理可知:![]()
根据双勾股定理可得:![]()
∴![]()
解得:![]() ,即
,即![]()
∴此时![]()
综上所述:t=![]() 或
或![]() 或
或![]() -3
-3

【题目】小华是数学兴趣小组的一名成员,他在学过二次函数的图像与性质之后,对![]() 的图像与性质进行了探究,探究过程如下,请你补充完整.
的图像与性质进行了探究,探究过程如下,请你补充完整.
(1)小刚通过计算得到几组对应的数值如下
| … |
|
|
|
|
|
| 0 | 1 |
| 2 | 3 | 4 | 5 | … |
| … |
| 0 | 4 | 6 |
| 6 | 4 | 6 |
| 6 | 4 | 0 |
| … |
填空:自变量的取值范围是__________________,![]() __________.
__________.
(2)在如图所示的平面直角坐标系中,描出上表中各组对应数值的点,并根据描出的点,画出该函数的图像.
(3)请你根据画出的图像,写出此函数的两条性质;
①__________________________________________;
②__________________________________________.
(4)直线![]() 经过
经过![]() ,若关于
,若关于![]() 的方程
的方程![]() 有4个不相等的实数根,则
有4个不相等的实数根,则![]() 的取值范围为_________.
的取值范围为_________.