题目内容
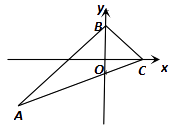
【题目】如图.已知曲线是由顶点为T的二次函数 
的图象旋转45度得到，直线AB： 
交曲线于C，D两点.
（1）线段AT长为,
（2）在y轴上有一点P，且PC+PD 为最小，则点P的坐标为
【答案】
（1）
（2）(0. 
)
【解析】解（1）依题可得：旋转前T点坐标为（0，1），
∵已知曲线是由顶点为T的二次函数 y =
x 2 + 1 的图象旋转45度得到，
∴OP=OT=1，
∴T（
，），
又∵直线AB： x =
交曲线于C，D两点，
∴A（，0），
∴AT=
=.
所以答案是：.
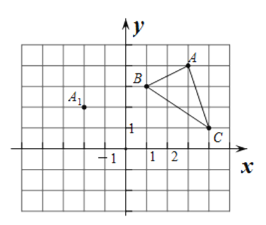
（2）求出D点关于y=-x的对称点，设对称点D‘（x'，y'）
可列式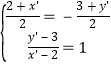
解得：D‘（-3，-2）
过C、D'画出直线，由C、D'的坐标求出函数关系。设y=kx+b
解得：
过CD’的直线为y=-11x-35
直线y=-11x-35与直线y=-x的交点即为P点
两式联立得：x=
，y=
可求出OP的长度为OP=
=
所以P点在原坐标系中的坐标为（0，）
【考点精析】根据题目的已知条件，利用二次函数的性质和旋转的性质的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．
阅读快车系列答案
【题目】某公司销售一种进价为20元/个的计算器，其销售量y（万个）与销售价格x（元/个）的变化如下表：
价格x（元/个） | … | 30 | 40 | 50 | 60 | … |
销售量y（万个） | … | 5 | 4 | 3 | 2 | … |
同时，销售过程中的其他开支（不含进价）总计40万元．
（1）观察并分析表中的y与x之间的对应关系，用所学过的一次函数，反比例函数或二次函数的有关知识写出y（万个）与x（元/个）的函数解析式．
（2）求出该公司销售这种计算器的净利润z（万元）与销售价格x（元/个）的函数解析式，销售价格定为多少元时净利润最大，最大值是多少？
（3）该公司要求净利润不能低于40万元，请写出销售价格x（元/个）的取值范围，若还需考虑销售量尽可能大，销售价格应定为多少元？
