题目内容
观察下列各式,并解答下面问题.
x2-1=(x-1)(x+1)
x3-1+(x-1)(x2+x+1)
x4-1=(x-1)(x3+x2+x+1)
x5-1=(x-1)(x4+x3+x2+x+1)
(1)根据上述规律:xn+1-1=
(2)请用上述规律公式因式分解:x2015-1.
x2-1=(x-1)(x+1)
x3-1+(x-1)(x2+x+1)
x4-1=(x-1)(x3+x2+x+1)
x5-1=(x-1)(x4+x3+x2+x+1)
(1)根据上述规律:xn+1-1=
(2)请用上述规律公式因式分解:x2015-1.
考点:因式分解-运用公式法
专题:规律型
分析:(1)根据提取公因式(x-1),可分解因式;
(2)根据提取公因式(x-1),可分解因式.
(2)根据提取公因式(x-1),可分解因式.
解答:解:(1)xn+1-1=(x-1)(xn+xn-1+xn-2+…x+1),
(2)x2015-1=(x-1)(x2014+x2013+x2012+…x+1)
故答案为:(x-1)(xn+xn-1+xn-2+…x+1).
(2)x2015-1=(x-1)(x2014+x2013+x2012+…x+1)
故答案为:(x-1)(xn+xn-1+xn-2+…x+1).
点评:本题考查了因式分解,利用了提公因式法分解因式.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知线段点A、B、C在一条直线上,AB=5,BC=3,则AC的长为( )
| A、8 | B、2 | C、8或2 | D、无法确定 |
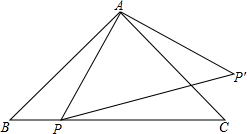 如图,△ABC是等腰三角形,点P是斜边AB上一点,将△CAP绕点C逆时针旋转90°至△CBP′的位置,若AC=2
如图,△ABC是等腰三角形,点P是斜边AB上一点,将△CAP绕点C逆时针旋转90°至△CBP′的位置,若AC=2 用直尺和圆规作一个角等于∠MON.(不写步骤,保留作图痕迹)
用直尺和圆规作一个角等于∠MON.(不写步骤,保留作图痕迹) 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF. 如图,∠C是△ABD边BD上的高,BC=15cm,∠BAC=30°,∠DAC=45°,求AD的长.
如图,∠C是△ABD边BD上的高,BC=15cm,∠BAC=30°,∠DAC=45°,求AD的长.