题目内容
3.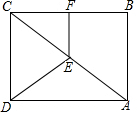 如图,E是矩形ABCD的对角线AC的中点,F是BC的中点,若AB=6,AD=8,则四边形CDEF的周长是( )
如图,E是矩形ABCD的对角线AC的中点,F是BC的中点,若AB=6,AD=8,则四边形CDEF的周长是( )| A. | 18 | B. | 19 | C. | 20 | D. | 23 |
分析 由矩形的性质和勾股定理求出AC,再证明EF是△ABC的中位线,得出EF=$\frac{1}{2}$AB=3,即可得出四边形ABOM的周长.
解答 解:解:如图所示:
∵四边形ABCD是矩形,
∴∠B=∠ADC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵E是AC的中点,
∴DE=$\frac{1}{2}$AC=5,
∵F是BC的中点,
∴CF=$\frac{1}{2}$CB=4,EF是△ABD的中位线,
∴EF=$\frac{1}{2}$AB=3,
∴四边形CDEF的周长=CD+DE+EF+CF=6+5+3+4=18.
故选A.
点评 本题考查了矩形的性质、三角形中位线定理、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
13. 如图,AB∥CD,∠1=50°,∠2的度数是( )
如图,AB∥CD,∠1=50°,∠2的度数是( )
 如图,AB∥CD,∠1=50°,∠2的度数是( )
如图,AB∥CD,∠1=50°,∠2的度数是( )| A. | 50° | B. | 100° | C. | 130° | D. | 140° |
11.下列计算正确的是( )
| A. | a3+a3=a6 | B. | (a2)3÷a4=a2 | C. | a5•a2=a10 | D. | a7÷a4•a2=a |
18.已知关于x,y的方程组$\left\{\begin{array}{l}{2x+y=k+1}\\{x+2y=2}\end{array}\right.$的解满足x+y<0,则k的取值范围是k<-3.
15.掷一枚质地均匀的骰子一次出现下列事件,其中的必然事件为( )
| A. | 掷出的点数是1 | B. | 掷出的点数是偶数 | ||
| C. | 掷出的点数是奇数 | D. | 掷出的点数小于7 |
12.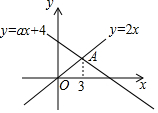 如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )| A. | x≥$\frac{3}{2}$ | B. | x≥3 | C. | x$≤\frac{3}{2}$ | D. | x≤3 |
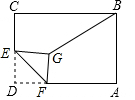 如图,在矩形ABCD中,AB=2,BC=4,E是CD的中点,F是AD上的动点,将∠DEF沿EF所在的直线折叠,得到△D′EF,连接BD′,则BD′的最小值是$\sqrt{17}$-1.
如图,在矩形ABCD中,AB=2,BC=4,E是CD的中点,F是AD上的动点,将∠DEF沿EF所在的直线折叠,得到△D′EF,连接BD′,则BD′的最小值是$\sqrt{17}$-1.