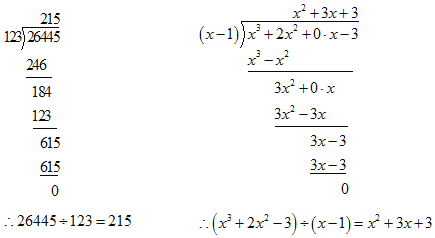��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���O������ԭ�㣬OA��OC�ֱ���x�ᡢy����������ϣ���OA��5��OC��4��
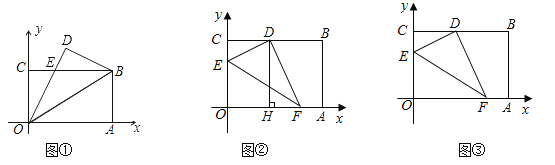
(1)��ͼ�٣��������ضԽ���OB�۵���ʹ�õ�A���ڵ�D����OD��CB�ཻ�ڵ�E�������ص�������OBE��ʲô�����Σ�˵��������ɣ��������������ε������
(2)��ͼ�ڣ���E��F�ֱ���OC��OA���ϵĵ㣬����OEF��EF�۵���ʹ�õ�O��������BC���ϵ�D�㣬����D��DH��OA����EF�ڵ�G����OA�ڵ�H����CD��2�����G�����ꣻ
(3)��ͼ�ۣ���(2)������������E��F��OC��OA���ƶ�ʱ����DҲ�ڱ�BC����֮�ƶ�����ֱ��д��BD��ȡֵ��Χ��
���𰸡���1��![]() �ǵ��������Σ����ɼ�������
�ǵ��������Σ����ɼ�������![]() ����2��
����2��![]() ����3��1��BD��3
����3��1��BD��3
��������
��1�������۵������ʺ;��ε����ʣ��ó�![]() ��
��![]() �������õ�
�������õ�![]() �ǵ��������Σ������ù��ɶ������EB�ij���������������ɣ�
�ǵ��������Σ������ù��ɶ������EB�ij���������������ɣ�
��2���õ�G�ĺ�����Ϊ2�������۵������ʺ�DH��OA���ó�![]() ������
������![]() �����ù��ɶ������DG�ij����ɵõ���G�������ꣻ
�����ù��ɶ������DG�ij����ɵõ���G�������ꣻ
��3��������������ǣ��ٵ���E�˶������C�غ�ʱ���ڵ���F�˶������A�غ�ʱ���ֱ����BD��ֵ�����ɵõ�BD��ȡֵ��Χ��
��1��![]() �ǵ��������Σ��������£�
�ǵ��������Σ��������£�
����ͼ��
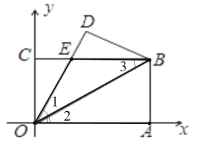
![]() ͼ���۵�
ͼ���۵�
![]()
![]() ����
����![]()
![]()
��![]()
![]()
![]()
![]() �ǵ���������
�ǵ���������
��![]() ����
����![]()
��![]() ��
�У�![]()
���![]()
![]()
��2������ͼ��
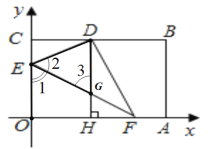
��ͼ���۵�
![]()
![]()
![]()
![]()
![]()
![]() ��
��![]() �ǵ���������
�ǵ���������
��![]() ����
����![]()
��![]() ��
��
![]() �����
�����![]()
![]()
��![]()
��3���ٵ���E�˶������C�غ�ʱ������ͼ��
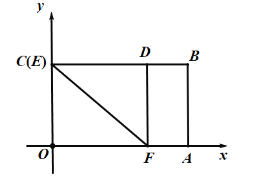
��ʱ��CD=OC=4����BD=BC-CD=1��
�ڵ���F�˶������A�غ�ʱ������ͼ��
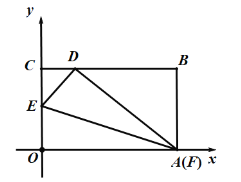
��ʱ��AD=OA=5����Rt��ABD�У�BD=![]() =
=![]() =3��
=3��
��BD��ȡֵ��ΧΪ1��BD��3.

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�����Ŀ��ijУ������ǿ��ë������ƹ���������������������˶���ÿλͬѧ������ֻ��ѡ��һ�������˶����Ը�Уѧ�������ȡ![]() ���е��飬���ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
���е��飬���ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
�˶���Ŀ | Ƶ��(����) |
��� | 30 |
���� |
|
ƹ���� | 36 |
���� |
|
���� | 12 |

����������ͼ����Ϣ����������⣺
(1)Ƶ���ֲ����е�![]() ��
��![]() ��
��
(2)������ͳ��ͼ�У����������ڵ����ε�Բ�Ľ�Ϊ ����
(3)ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���
����Ŀ��ij�дӲ�ͬѧУ�����ȡ100������������ʹ����ѧ�̸�����IJ��������е��飬ͳ�ƽ�����£�
���� | 0 | 1 | 2 | 3 |
���� | 10 | 20 | 30 | 40 |
�����������ݣ�����˵����ȷ���ǣ�������
A.������2��B.�����2��
C.ƽ������3��D.������1.5