题目内容
以直角三角形的三边为边长分别向三角形外作正方形，若其中两个较小正方形的面积是25，36，则最大一个正方形的面积是
- A.61
- B.11
- C.121
- D.1921
A
分析：结合正方形的面积公式和勾股定理，得最大正方形的面积等于两个较小的正方形的面积．
解答：根据题意，得
最大正方形的面积=25+36=61．
故选A．
点评：注意：以直角三角形的两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积．
分析：结合正方形的面积公式和勾股定理，得最大正方形的面积等于两个较小的正方形的面积．
解答：根据题意，得
最大正方形的面积=25+36=61．
故选A．
点评：注意：以直角三角形的两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
7、如图，以直角三角形的三边为边向三角形外作正方形，已知甲、乙两个正方形的面积分别为4、6，则丙正方形的面积为
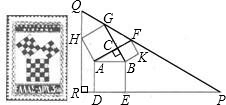
如图，在Rt△ABC中，∠C=Rt∠，分别以直角三角形的三边为直径作三个半圆，则S1、S2、S3之间的关系：