题目内容
直角三角形的面积为6，两直角边的和为7，则斜边长为（ ）
A、
| ||
| B、5 | ||
C、
| ||
| D、7 |
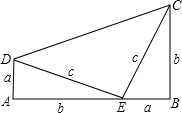
分析：设两直角边长为a和b，则a+b=7，ab=12，联立方程组解方程组即可求得三角形的直角边的长，再利用勾股定理求得斜边的长．
解答：解：设两直角边长为a和b，则
解方程组得a=3，b=4或b=3，a=4，
所以斜边c=
=
=5．
故选B．
|
解方程组得a=3，b=4或b=3，a=4，
所以斜边c=
| a2+b2 |
| 32+42 |
故选B．
点评：准确应用直角三角形三边关系．熟练掌握勾股定理的运用．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
斜边长为2，两直角边之和为（
+1）的直角三角形的面积为（ ）
| 3 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、2（
|
