ћвƒњƒЏ»Ё
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђµг![]() ќ™„ш±к‘≠µг£ђ≈„ќпѕя
ќ™„ш±к‘≠µг£ђ≈„ќпѕя![]() ”л
”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђµг
£ђµг![]() £ђ”л
£ђ”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђЅђљ”
£ђЅђљ”![]() £ђµг
£ђµг![]() ‘ЏµЏґюѕуѕёµƒ≈„ќпѕя…ѕ£ђЅђљ”
‘ЏµЏґюѕуѕёµƒ≈„ќпѕя…ѕ£ђЅђљ”![]() £ђѕяґќ
£ђѕяґќ![]() љїѕяґќ
љїѕяґќ![]() ”Џµг
”Џµг![]() £Ѓ
£Ѓ
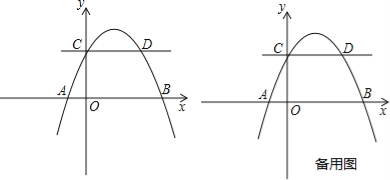
£®1£©«у≈„ќпѕяµƒ±ніп љ£ї
£®2£©»ф![]() µƒ√жїэќ™
µƒ√жїэќ™![]() £ђ
£ђ![]() µƒ√жїэќ™
µƒ√жїэќ™![]() µ±
µ±![]() ±£ђ«уµг
±£ђ«уµг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
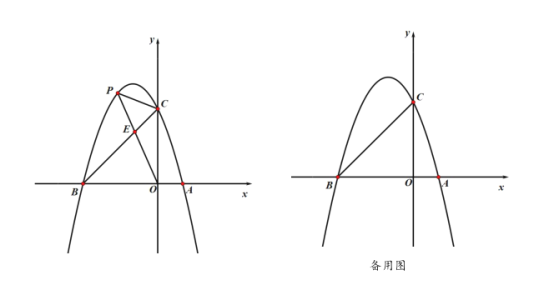
£®3£©“—÷™µг![]() єЎ”Џ≈„ќпѕяґ‘≥∆÷бµƒґ‘≥∆µгќ™µг
єЎ”Џ≈„ќпѕяґ‘≥∆÷бµƒґ‘≥∆µгќ™µг![]() £ђЅђљ”
£ђЅђљ”![]() £ђµг
£ђµг![]() ‘Џ
‘Џ![]() ÷б…ѕ£ђµ±
÷б…ѕ£ђµ±![]() ±£ђ
±£ђ
Ґў«у¬ъ„гћхЉюµƒЋщ”–µг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
ҐЏµ±µг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ ±£ђµг
…ѕ ±£ђµг![]() «ѕяґќ
«ѕяґќ![]() Ќв“їµг£ђ
Ќв“їµг£ђ![]() £ђЅђљ”
£ђЅђљ”![]() £ђљЂѕяґќ
£ђљЂѕяґќ![]() »∆„≈µг
»∆„≈µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() £ђµ√µљѕяґќ
£ђµ√µљѕяґќ![]() £ђЅђљ”
£ђЅђљ”![]() £ђ÷±љ”–і≥цѕяґќ
£ђ÷±љ”–і≥цѕяґќ![]() µƒ»°÷µЈґќІ£Ѓ
µƒ»°÷µЈґќІ£Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®2£©
£ї£®2£©![]() їт
їт![]() £ї£®3£©Ґў
£ї£®3£©Ґў![]() їт
їт![]() £їҐЏ
£їҐЏ![]()
°Њљвќц°њ
£®1£©љЂµгA°ҐB„ш±кіъ»лљвќц љљвірЉіњ…£ї
£®2£©ѕ»«у≥цµгCµƒ„ш±кќ™£®0,3£©£ђєэµгC„чCG°ЌOP”ЏG£ђЄщЊЁ![]() £ђ
£ђ![]() £ђ
£ђ![]() µ√µљ
µ√µљ![]() £ђєэµгP„чPF°Ќx÷б”ЏF£ђєэµгE„чEN°ЌPF”ЏN£ђµ√µљ
£ђєэµгP„чPF°Ќx÷б”ЏF£ђєэµгE„чEN°ЌPF”ЏN£ђµ√µљ![]() £ђ…иµгPµƒ„ш±кќ™£®a£ђ
£ђ…иµгPµƒ„ш±кќ™£®a£ђ![]() £©£ђ«у≥ц÷±ѕяBCµƒљвќц љќ™y=x+3£ђµ√µљE£®
£©£ђ«у≥ц÷±ѕяBCµƒљвќц љќ™y=x+3£ђµ√µљE£®![]() £ђ
£ђ![]() +3£©£ђЄщЊЁ2PF=5PNµ√µљ5(
+3£©£ђЄщЊЁ2PF=5PNµ√µљ5(![]() -
-![]() -3)=2(
-3)=2(![]() )£ђ«у≥цx÷µЉіњ…µ√µљµгPµƒ„ш±к£ї
)£ђ«у≥цx÷µЉіњ…µ√µљµгPµƒ„ш±к£ї
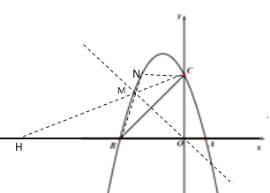
£®3£©Ґўѕ»«у≥ц≈„ќпѕяµƒґ‘≥∆÷б «÷±ѕяx=-1£ђµ√µљN£®-2,3£©£ђ«у≥ц÷±ѕяBNµƒљвќц љќ™y=3x+9£ђЈ÷Ѕљ÷÷«йњц£Їµ±µгH‘ЏOB÷ЃЉд ±£ђ”…![]() £ђµ√µљBN°ќCH£ђµ√µљ÷±ѕяCHµƒљвќц љќ™y=3x+3£ђЉіњ…«у≥цµгHµƒ„ш±кќ™£®-1,0£©£їµ±µгH‘ЏµгB„у≤а ±£ђCHљїBN”ЏM£ђ„ч÷±ѕяOM£ђ”…
£ђµ√µљBN°ќCH£ђµ√µљ÷±ѕяCHµƒљвќц љќ™y=3x+3£ђЉіњ…«у≥цµгHµƒ„ш±кќ™£®-1,0£©£їµ±µгH‘ЏµгB„у≤а ±£ђCHљїBN”ЏM£ђ„ч÷±ѕяOM£ђ”…![]() µ√µљBM=MC£ђє OM «BCµƒіє÷±∆љЈ÷ѕя£ђ«у≥цљїµгMµƒ„ш±кќ™£®-
µ√µљBM=MC£ђє OM «BCµƒіє÷±∆љЈ÷ѕя£ђ«у≥цљїµгMµƒ„ш±кќ™£®-![]() £ђ
£ђ![]() £©£ђ‘ў«у≥ц÷±ѕяCMµƒљвќц љќ™y=
£©£ђ‘ў«у≥ц÷±ѕяCMµƒљвќц љќ™y=![]() x+3£ђЉіњ…µ√µљµгHµƒ„ш±кќ™£®-9,0£©£їҐЏ»зЌЉ1£ђµ±µгQ‘Џx÷бѕ¬Јљ«“MH°Ќx÷б ±£ђMH„о–°£ђ„чQG°Ќx÷б£ђєэµгM„чMF°ЌQG”ЏF£ђ‘тЋƒ±я–ќMHGF «ЊЎ–ќ£ђ÷§√ч°чBQG°’°чQMF£ђµ√µљFM=GQ£ђBG=FQ£ђјы”√єіє…ґ®јн«у≥цGQ=GH=
x+3£ђЉіњ…µ√µљµгHµƒ„ш±кќ™£®-9,0£©£їҐЏ»зЌЉ1£ђµ±µгQ‘Џx÷бѕ¬Јљ«“MH°Ќx÷б ±£ђMH„о–°£ђ„чQG°Ќx÷б£ђєэµгM„чMF°ЌQG”ЏF£ђ‘тЋƒ±я–ќMHGF «ЊЎ–ќ£ђ÷§√ч°чBQG°’°чQMF£ђµ√µљFM=GQ£ђBG=FQ£ђјы”√єіє…ґ®јн«у≥цGQ=GH=![]() £ђµ√µљMH=FG=BG-FG=
£ђµ√µљMH=FG=BG-FG=![]() £ї»зЌЉ2£ђµ±µгQ‘Џx÷б…ѕЈљ£ђ«“MH°Ќx÷б ±£ђMH„оіу£ђєэµгQ„чQG°Ќx÷б£ђQF°ЌMH”ЏF£ђ‘тЋƒ±я–ќHGQF «ЊЎ–ќ£ђЌђјн£Ї°чBGQ°’°чMFQ£ђµ√µљQG=FQ=HG£ђBG=MF£ђјы”√єіє…ґ®јн«у≥цGQ=GH=
£ї»зЌЉ2£ђµ±µгQ‘Џx÷б…ѕЈљ£ђ«“MH°Ќx÷б ±£ђMH„оіу£ђєэµгQ„чQG°Ќx÷б£ђQF°ЌMH”ЏF£ђ‘тЋƒ±я–ќHGQF «ЊЎ–ќ£ђЌђјн£Ї°чBGQ°’°чMFQ£ђµ√µљQG=FQ=HG£ђBG=MF£ђјы”√єіє…ґ®јн«у≥цGQ=GH=![]() £ђµ√µљMH=BG+FH=
£ђµ√µљMH=BG+FH=![]() £ђЉіњ…µ√µљMHµƒ»°÷µЈґќІ.
£ђЉіњ…µ√µљMHµƒ»°÷µЈґќІ.
£®1£©љЂµгA°ҐBµƒ„ш±кіъ»л![]() ÷–£ђµ√
÷–£ђµ√
![]() £ђљвµ√
£ђљвµ√![]() £ђ
£ђ
°а≈„ќпѕяµƒ±ніп љќ™![]() £ї
£ї
£®2£©µ±x=0 ±£ђy=3£ђ°аµгCµƒ„ш±кќ™£®0,3£©£ђ
єэµгC„чCG°ЌOP”ЏG£ђ
°я![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
°а![]() £ђ
£ђ
°а![]() £ђ
£ђ
єэµгP„чPF°Ќx÷б”ЏF£ђєэµгE„чEN°ЌPF”ЏN£ђ
°аEN°ќOF£ђ
°а![]() ,
,
…иµгPµƒ„ш±кќ™£®a£ђ![]() £©£ђ
£©£ђ
°аOF=-a£ђEN=-![]() £ђ
£ђ
°аµгEµƒЇб„ш±кќ™![]() £ђ
£ђ
°яB£®3,0£©£ђC£®0,3£©£ђ
°а÷±ѕяBCµƒљвќц љќ™y=x+3£ђ
µ±x=![]() ±£ђy=
±£ђy=![]() +3£ђ
+3£ђ
°аE£®![]() £ђ
£ђ![]() +3£©£ђ
+3£©£ђ
°я2PF=5PN£ђ
°а5(![]() -
-![]() -3)=2(
-3)=2(![]() ),
),
љвµ√![]() £ђ
£ђ![]() £ђ
£ђ
°аµгPµƒ„ш±кќ™£®-1,4£©їт£®-2,3£©£ї
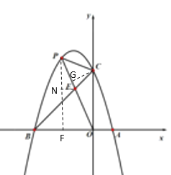
£®3£©Ґў°я![]()
![]() £ђ
£ђ
°а≈„ќпѕяµƒґ‘≥∆÷б «÷±ѕяx=-1£ђ
°яµг![]() єЎ”Џ≈„ќпѕяґ‘≥∆÷бµƒґ‘≥∆µгќ™µг
єЎ”Џ≈„ќпѕяґ‘≥∆÷бµƒґ‘≥∆µгќ™µг![]() £ђC£®0,3£©£ђ
£ђC£®0,3£©£ђ
°аN£®-2,3£©£ђ
…и÷±ѕяBNµƒљвќц љќ™y=kx+b£ђ
°а![]() £ђљвµ√
£ђљвµ√![]() £ђ
£ђ
°а÷±ѕяBNµƒљвќц љќ™y=3x+9£ђ
µ±µгH‘ЏOB÷ЃЉд ±£ђ»зЌЉ£ђ
°я![]() £ђ
£ђ
°аBN°ќCH£ђ
…и÷±ѕяCHµƒљвќц љќ™y=3x+m£ђљЂµгCµƒ„ш±кіъ»л£ђµ√m=3,
°а÷±ѕяCHµƒљвќц љќ™y=3x+3£ђ
µ±y=0 ±£ђµ√x=-1£ђ
°аµгHµƒ„ш±кќ™£®-1,0£©£ї
µ±µгH‘ЏµгB„у≤а ±£ђ»зЌЉ£ђCHљїBN”ЏM£ђ„ч÷±ѕяOM£ђ
°я![]() £ђ
£ђ
°аBM=MC£ђ
°яOB=OC£ђ
°аOM «BCµƒіє÷±∆љЈ÷ѕя£ђ
°а÷±ѕяOMµƒљвќц љќ™y=-x£ђ
љвЈљ≥ћ„й![]() £ђµ√
£ђµ√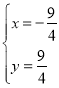 £ђ
£ђ
°аµгMµƒ„ш±кќ™£®-![]() £ђ
£ђ![]() £©£ђ
£©£ђ
…и÷±ѕяCMµƒљвќц љќ™y=cx+n£ђ
°а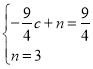 £ђ°а
£ђ°а![]() £ђ
£ђ
°а÷±ѕяCMµƒљвќц љќ™y=![]() x+3£ђ
x+3£ђ
µ±y=0 ±x=-9£ђ°аµгHµƒ„ш±кќ™£®-9,0£©£ђ
„џ…ѕ£ђµ±![]() ±£ђµгHµƒ„ш±кќ™£®-1,0£©їт£®-9£ђ0£©£ї
±£ђµгHµƒ„ш±кќ™£®-1,0£©їт£®-9£ђ0£©£ї
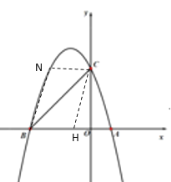
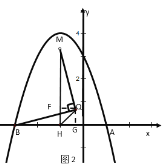
ҐЏ»зЌЉ1£ђµ±µгQ‘Џx÷бѕ¬Јљ«“MH°Ќx÷б ±£ђMH„о–°£ђ„чQG°Ќx÷б£ђєэµгM„чMF°ЌQG”ЏF£ђ‘тЋƒ±я–ќMHGF «ЊЎ–ќ£ђ
°аFM=GH£ђFG=MH£ђ
°я°ѕBQM=°ѕF=90°г£ђ
°а°ѕBQG+°ѕFQM=°ѕFMQ+°ѕFQM=90°г£ђ
°а°ѕBQG=°ѕFMQ£ђ
°я°ѕBGQ=°ѕF£ђBQ=MQ£ђ
°а°чBQG°’°чQMF£ђ
°аFM=GQ£ђBG=FQ£ђ
°аGQ=FM=GH£ђ
°яQH=1£ђ
°аGQ=GH=![]() £ђ
£ђ
°а MH=FG=BG-FG=![]() £ї
£ї
»зЌЉ2£ђµ±µгQ‘Џx÷б…ѕЈљ£ђ«“MH°Ќx÷б ±£ђMH„оіу£ђєэµгQ„чQG°Ќx÷б£ђQF°ЌMH”ЏF£ђ‘тЋƒ±я–ќHGQF «ЊЎ–ќ£ђ
°аFQ=HG£ђFH=QG£ђ
Ќђјн£Ї°чBGQ°’°чMFQ£ђ
°аQG=FQ=HG£ђBG=MF£ђ
°яQH=1£ђ
°аGQ=GH=![]() £ђ
£ђ
°аMH=BG+FH=![]() £ђ
£ђ
°аMHµƒ»°÷µЈґќІ «![]() .
.


 –°ћм≤≈њќ ±„ч“µѕµЅ–ір∞Є
–°ћм≤≈њќ ±„ч“µѕµЅ–ір∞Є “їњќЋƒЅЈѕµЅ–ір∞Є
“їњќЋƒЅЈѕµЅ–ір∞Є ї∆Є‘–°„і‘™¬ъЈ÷≥еіћќҐ≤в—йѕµЅ–ір∞Є
ї∆Є‘–°„і‘™¬ъЈ÷≥еіћќҐ≤в—йѕµЅ–ір∞Є –¬Є®љћµЉ—ІѕµЅ–ір∞Є
–¬Є®љћµЉ—ІѕµЅ–ір∞Є —фєвЌђ—І“їѕя√ы ¶»Ђ”≈Ї√ЊнѕµЅ–ір∞Є
—фєвЌђ—І“їѕя√ы ¶»Ђ”≈Ї√ЊнѕµЅ–ір∞Є