题目内容

分母有理化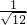：数学公式=________； 数学公式=________（a＞0）．

    
分析：利用二次根式的性质，即可将各二次根式化简，注意分母有理化常常是乘二次根式本身（分母只有一项）或与原分母组成平方差公式．
解答：==；
=．
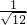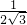故答案为：，．
点评：此题考查了分母有理化的知识．此题比较简单，注意将各二次根式化为最简二次根式是解此题的关键．
练习册系列答案
相关题目
观察下列分母有理化的计算：
1
2
+
1
=
2
-
1

1
3
+
2
=
3
-
2

1
4
+
3
=
4
-
3

1
5
+
4
=
5
-
4

…从计算结果中找出规律，并利用这一规律计算：（
1
2
+
1
+
1
3
+
2
+
1
4
+
3
+…+
1
2002
+
2001

）（
2002
+1）=
 
．
观察下列分母有理化的计算：
1
2
+1
=
2
-1，
1
3
+
2
=
3
-
2
，
1
4
-
3
=
4
-
3
，
1
5
+
4
=
5
-
4
，.．在计算结果中找出规律，用含字母n（n表示大于0的自然数）表示；
再利用这一规律计算下列式子的值：(
1
2
+
1
+
1
3
+
2
+
1
4
+
3
+…+
1
2007
+
2006
)(
2007
+1)的值．
把下列各式分母有理化：
（1）
2
3
48
；（2）
3
a+2
；
（3）
2
5
-
3
；（4）
x-y
x
+
y
；
（5）
x-2+
x2-4
x+2+
x2-4
(x＞2)．
观察下列各式，通过分母有理化，把不是最简二次根式的化成最简二次根式：
1
2
+1
=
1×(
2
-1)
(
2
+1)(
2
-1)
=
2
-1
2-1
=
2
-1，
1
3
+
2
=
1×(
3
-
2
)
(
3
+
2
)(
3
-
2
)
=
3
-
2
3-2
=
3
-
2
，
同理可得：
1
4
+
3
=
4
-
3
，…
从计算结果中找出规律，并利用这一规律计算
（
1
2
+1
+
1
3
+
2
+
1
4
+
3
+…
1
2010
+
2009
）（
2010
+1）的值．
分母有理化：
2
3-
7
=
3+
7
3+
7
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网