Question

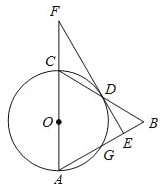
【题目】如图，在△ABC中，以AC边为直径作⊙O交BC边于点D，交AB于点G，且D是BC中点，DE⊥AB，交AB于点E，交AC的延长线交于点F．

（1）求证：直线EF是⊙O的切线．

（2）若CF=3，cos∠CAB=，求⊙O的半径和线段BD的长．

Answer 1

【答案】（1）证明见解析；（2）⊙O的半径为，BD的长为．

【解析】

（1）根据三角形的中位线定理证明OD∥AB，可得OD⊥EF，所以直线EF是⊙O的切线；

（2）设⊙O的半径为r，根据cos∠FOD=cos∠CAB=，求得r的值，根据平行线分线段成比例定理得：，可得AE的长，并计算BE的长，证明△BDE∽△BAD，则，代入可得BD的长．

（1）证明：连接OD．

∵OA=OC，DB=DC，∴OD∥AB．

∵DE⊥AB，∴OD⊥EF，∴直线EF是⊙O的切线．

（2）如图，连接AD，设⊙O的半径为r．

在Rt△ODF中，∵cos∠FOD=cos∠CAB====，∴r=，∴AB=2DO=9．

∵OD∥AB，∴，即=，AE=，∴BE=AB﹣AE=9﹣=．

∵AC为⊙O的直径，∴∠ADE+∠BDE=∠ADB=90°．

∵DE⊥AB，∴∠B+∠BDE=90°，∴∠ADE=∠B，∴△BDE∽△BAD，∴，∴BD2=ABBE，∴BD2=9×=，∴BD=，∴⊙O的半径为，BD的长为．