题目内容
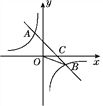
【题目】如图,一次函数![]() 的图象与
的图象与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.动点
轴对称.动点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上(点
上(点![]() 与点
与点![]() ,
,![]() 不重合),且满足
不重合),且满足![]() .
.
(1)求点![]() ,
,![]() 的坐标及线段
的坐标及线段![]() 的长度;
的长度;
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由;
,说明理由;
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)10;(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点![]() ,
,![]() 的坐标,结合点
的坐标,结合点![]() 与点
与点![]() 关于
关于![]() 轴对称可得出点
轴对称可得出点![]() 的坐标,进而可得出线段
的坐标,进而可得出线段![]() 的长度;
的长度;
(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ,由点
,由点![]() ,
,![]() 的坐标可得出
的坐标可得出![]() 的长度,由勾股定理可求出
的长度,由勾股定理可求出![]() 的长度,进而可得出
的长度,进而可得出![]() ,通过角的计算及对称的性质可得出
,通过角的计算及对称的性质可得出![]() ,
,![]() ,结合
,结合![]() 可证出
可证出![]() ,由此可得出:当点
,由此可得出:当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ;
;
(3)分![]() ,
,![]() 及
及![]() 三种情况考虑:①当
三种情况考虑:①当![]() 时,由(2)的结论结合全等三角形的性质可得出当点
时,由(2)的结论结合全等三角形的性质可得出当点![]() 的坐标是
的坐标是![]() 时
时![]() ;②当
;②当![]() 时,利用等腰三角形的性质结合
时,利用等腰三角形的性质结合![]() 可得出
可得出![]() ,利用三角形外角的性质可得出
,利用三角形外角的性质可得出![]() ,进而可得出此种情况不存在;③当
,进而可得出此种情况不存在;③当![]() 时,利用等腰三角形的性质结合
时,利用等腰三角形的性质结合![]() 可得出
可得出![]() ,设此时
,设此时![]() 的坐标是
的坐标是![]() ,在
,在![]() 中利用勾股定理可得出关于
中利用勾股定理可得出关于![]() 的一元一次方程,解之即可得出结论.综上,此题得解.
的一元一次方程,解之即可得出结论.综上,此题得解.
解:(1)当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() .
.
(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ,理由如下:
,理由如下:
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]()
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 和
和![]() 关于
关于![]() 轴对称,
轴对称,
![]() .
.
在![]() 和
和![]() 中
中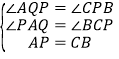 ,
,
![]() .
.
![]() 当点
当点![]() 的坐标是
的坐标是![]() 时,
时,![]() .
.
(3)分为三种情况:
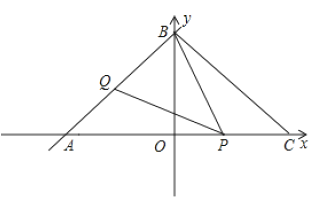
①当![]() 时,如图1所示,由(2)知,当点
时,如图1所示,由(2)知,当点![]() 的坐标是
的坐标是![]() 时,
时,
![]()
![]() ,
,
![]() 此时
此时![]() 点的坐标是
点的坐标是![]() ;
;
②当![]() 时,则
时,则![]() ,
,
![]() ,
,
![]() .
.
而根据三角形的外角性质得:![]() ,
,
![]() 此种情况不存在;
此种情况不存在;
③当![]() 时,则
时,则![]() ,
,
![]() ,如图2所示.
,如图2所示.
设此时![]() 的坐标是
的坐标是![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 此时
此时![]() 的坐标是
的坐标是![]() .
.
综上所述:当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.

练习册系列答案
相关题目