题目内容
20.顺次联结对角线相等的四边形各边中点所得到的四边形是( )| A. | 平行四边形 | B. | 矩形 | C. | 正方形 | D. | 菱形 |
分析 因为四边形的两条对角线相等,根据三角形的中位线定理,可得所得的四边形的四边相等,则所得的四边形是菱形.
解答 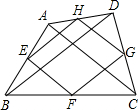 解:如图,AC=BD,E、F、G、H分别是线段AB、BC、CD、AD的中点,
解:如图,AC=BD,E、F、G、H分别是线段AB、BC、CD、AD的中点,
则EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知,EH=FG=$\frac{1}{2}$BD,EF=HG=$\frac{1}{2}$AC,
∵AC=BD,
∴EH=FG=FG=EF,
∴四边形EFGH是菱形.
故选D.
点评 本题考查了三角形的中位线定理,难度中等,需要掌握三角形的中位线平行于第三边,并且等于第三边的一半,另外要知道四边相等的四边形是菱形.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
10.下列各式能用平方差公式运算的是( )
| A. | (x+a)(x+a) | B. | (a+x)(a-b) | C. | (-x-b)(x+b) | D. | (-a+b)(-a-b) |
11.$-\sqrt{3}+1$的倒数是( )
| A. | $-\frac{{\sqrt{3}-1}}{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | $-\frac{{1+\sqrt{3}}}{2}$ | D. | $-\frac{{1-\sqrt{3}}}{2}$ |
15.(p-q)4÷(q-p)3=( )
| A. | p-q | B. | q-p | C. | -p-q | D. | p+q |
5.下列式子中,一定是二次根式的是( )
| A. | -$\sqrt{7}$ | B. | $\root{3}{7}$ | C. | $\sqrt{x}$ | D. | x |
12.下列分解因式正确的是( )
| A. | x2+y2=(x+y)(x-y) | B. | a2-9=(a+3)(a-3) | C. | (a+3)(a-3)=a2-9 | D. | x3-x=x(x2-1) |
9.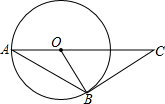 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )
 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )| A. | 50° | B. | 40° | C. | 25° | D. | 20度 |