题目内容
5. 如图,已知∠AOB=60°,点P在边OA上,OP=20,点M点N在边OB上,PM=PN.若MN=4,则OM等于8.
如图,已知∠AOB=60°,点P在边OA上,OP=20,点M点N在边OB上,PM=PN.若MN=4,则OM等于8.
分析 首先过点P作PD⊥OB于点D,利用直角三角形中30°所对边等于斜边的一半得出DO的长,再利用等腰三角形的性质求出OM的长.
解答 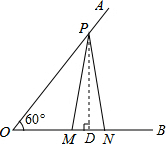 解:过点P作PD⊥OB于点D,
解:过点P作PD⊥OB于点D,
∵∠AOB=60°,PD⊥OB,OP=20,
∴DO=10,
∵PM=PN,MN=4,PD⊥OB,
∴MD=ND=2,
∴MO=8.
故答案为:8.
点评 此题主要考查了直角三角形中30°所对边等于斜边的一半得出DO的长以及等腰三角形的性质,得出OD的长是解题关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | x4•x4=x16 | B. | a2+a2=a4 | C. | (a6)2÷(a4)3=1 | D. | (a+b)2=a2+b2 |
20.在△ABC中,若∠A:∠B=5:7,且∠C比∠A大10°,那么∠C的度数为( )
| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
14.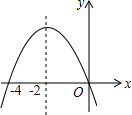 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
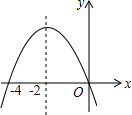 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )| A. | ①③④ | B. | ②④⑤ | C. | ①②⑤ | D. | ②③⑤ |
15.下列运算正确的是( )
| A. | 3a2•a3=3a6 | B. | 5x4-x2=4x2 | C. | (2a2)3•(-ab)=-8a7b | D. | 2x2÷2x2=0 |
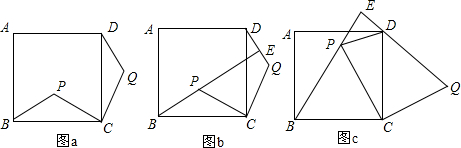
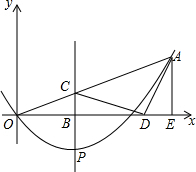 如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.