题目内容
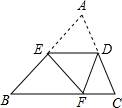 如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是
如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是
- A.50
- B.60
- C.70
- D.80
A
分析:根据翻折变换以及E为AB的中点,得出∠B=∠EFB= (180°-∠BEF),然后根据外角的知识得出∠AED=
(180°-∠BEF),然后根据外角的知识得出∠AED= (180°-∠BEF),则可证明ED∥BC,最后根据中位线的性质即可得出DE的长度.
(180°-∠BEF),则可证明ED∥BC,最后根据中位线的性质即可得出DE的长度.
解答:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AE=EF,
∵E是AB边的中点,
∴AE=EB,
∴BE=EF,
∴∠B=∠BFE= (180°-∠BEF),
(180°-∠BEF),
∵∠AEF=180°-∠BEF,∠AED=∠FED,
∴∠AED= (180°-∠BEF),
(180°-∠BEF),
∴∠AED=∠B,
∴ED∥BC,
∵E为AB的中点,
∴EF为BC的中位线,
∴EF= =
= =50.
=50.
故选A.
点评:本题考查了翻折变换的知识,难度一般,得出∠AED=∠B是解答本题的关键,注意掌握翻折变换的性质:翻折前后对应边相等、对应角相等.
分析:根据翻折变换以及E为AB的中点,得出∠B=∠EFB=
 (180°-∠BEF),然后根据外角的知识得出∠AED=
(180°-∠BEF),然后根据外角的知识得出∠AED= (180°-∠BEF),则可证明ED∥BC,最后根据中位线的性质即可得出DE的长度.
(180°-∠BEF),则可证明ED∥BC,最后根据中位线的性质即可得出DE的长度.解答:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AE=EF,
∵E是AB边的中点,
∴AE=EB,
∴BE=EF,
∴∠B=∠BFE=
 (180°-∠BEF),
(180°-∠BEF),∵∠AEF=180°-∠BEF,∠AED=∠FED,
∴∠AED=
 (180°-∠BEF),
(180°-∠BEF),∴∠AED=∠B,
∴ED∥BC,
∵E为AB的中点,
∴EF为BC的中位线,
∴EF=
 =
= =50.
=50.故选A.
点评:本题考查了翻折变换的知识,难度一般,得出∠AED=∠B是解答本题的关键,注意掌握翻折变换的性质:翻折前后对应边相等、对应角相等.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 16、如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF=
16、如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF= 16、如图,D是AB边上的中点,将△ABC沿过点D的直线DE折叠.使点A落在BC边上F处,若∠B=65°,则∠BDF=
16、如图,D是AB边上的中点,将△ABC沿过点D的直线DE折叠.使点A落在BC边上F处,若∠B=65°,则∠BDF= (2013•广东模拟)如图,D是AB边上的中点,将△ABC′沿过D的直线折叠,使点A落在BC上F处,若S△DEF=7.5cm2,A到BC的距离为6cm,∠B=45°,则FC=
(2013•广东模拟)如图,D是AB边上的中点,将△ABC′沿过D的直线折叠,使点A落在BC上F处,若S△DEF=7.5cm2,A到BC的距离为6cm,∠B=45°,则FC= (2013•竹溪县模拟)如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC边上F处,若∠B=40°,则∠ADF=
(2013•竹溪县模拟)如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC边上F处,若∠B=40°,则∠ADF= (2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( )
(2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( )