题目内容
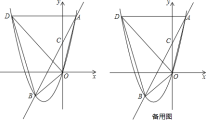
【题目】如图,二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
(1)求该二次函数的解析式;
(2)求点B坐标和坐标平面内使△EOD∽△AOB的点E的坐标;
(3)设点F是BD的中点,点P是线段DO上的动点,问PD为何值时,将△BPF沿边PF翻折,使△BPF与△DPF重叠部分的面积是△BDP的面积的![]() ?
?
【答案】(1) y=x2+3x(2)当点E的坐标是(8,﹣2)或(2,﹣8)时,△EOD∽△AOB;(3)PD=![]() 或PD=3
或PD=3![]()
【解析】
试题分析:(1)运用待定系数法和对称轴的关系式求出a、b的即可;
(2)由待定系数法求出直线AC的解析式,由抛物线的解析式构成方程组就可以求出B点的坐标,由相似三角形的性质及旋转的性质就可以得出E的坐标;
(3)分情况讨论当点B落在FD的左下方,点B,D重合,点B落在OD的右上方,由三角形的面积公式和菱形的性质的运用就可以求出结论.
试题解析:1)∵y=ax2+bx(a≠0)的图象经过点A(1,4),且对称轴是直线x=﹣![]() ,
,
∴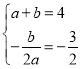 ,
,
解得:![]() ,
,
∴二次函数的解析式为y=x2+3x;
(2)如图1,

∵点A(1,4),线段AD平行于x轴,
∴D的纵坐标为4,
∴4=x2+3x,
∴x1=﹣4,x2=1,
∴D(﹣4,4).
设直线AC的解析式为y=kx+b,由题意,得
![]() ,
,
解得:![]() ,
,
∴y=2x+2;
当2x+2=x2+3x时,
解得:x1=﹣2,x2=1(舍去).
∴y=﹣2.
∴B(﹣2,﹣2).
∴DO=4![]() ,BO=2
,BO=2![]() ,BD=2
,BD=2![]() ,OA=
,OA=![]() .
.
∴DO2=32,BO2=8,BD2=40,
∴BO2+BO2=BD2,
∴△BDO为直角三角形.
∵△EOD∽△AOB,
∴∠EOD=∠AOB,![]() ,
,
∴∠EOD﹣∠AOB=∠AOB﹣∠AOB,
∴∠BOD=∠AOE=90°.
即把△AOB绕着O点顺时针旋转90°,OB落在OD上B′,OA落在OE上A1
∴A1(4,﹣1),
∴E(8,﹣2).
作△AOB关于x轴的对称图形,所得点E的坐标为(2,﹣8).
∴当点E的坐标是(8,﹣2)或(2,﹣8)时,△EOD∽△AOB;
(3)由(2)知DO=4![]() ,BO=2
,BO=2![]() ,BD=2
,BD=2![]() ,∠BOD=90°.
,∠BOD=90°.
若翻折后,点B落在FD的左下方,如图2.

S△HFP=![]() S△BDP=
S△BDP=![]() S△DPF=
S△DPF=![]() S△B′PF=S△DHP=S△B′HF,
S△B′PF=S△DHP=S△B′HF,
∴DH=HF,B′H=PH,
∴在平行四边形B′FPD中,PD=B′F=BF=![]() BD=
BD=![]() ;
;
若翻折后,点B,D重合,S△HFP=![]() S△BDP,不合题意,舍去.
S△BDP,不合题意,舍去.
若翻折后,点B落在OD的右上方,如图3,

S△HFP=![]() S△BDP=
S△BDP=![]() S△BPF=
S△BPF=![]() S△DPF=
S△DPF=![]() S△B′PF=S△DHF=S△B′HP
S△B′PF=S△DHF=S△B′HP
∴B′P=BP,B′F=BF.DH=HP,B′H=HF,
∴四边形DFPB′是平行四边形,
∴B′P=DF=BF,
∴B′P=BP=B′F=BF,
∴四边形B′FPD是菱形,
∴FD=B′P=BP=![]() BD=
BD=![]() ,根据勾股定理,得
,根据勾股定理,得
OP2+OB2=BP2,
∴(4![]() ﹣PD)2+(2
﹣PD)2+(2![]() )2=(
)2=(![]() )2,
)2,
PD=3![]() ,PD=5
,PD=5![]() >4
>4![]() (舍去),
(舍去),
综上所述,PD=![]() 或PD=3
或PD=3![]() 时,将△BPF沿边PF翻折,使△BPF与△DPF重叠部分的面积是△BDP的面积的
时,将△BPF沿边PF翻折,使△BPF与△DPF重叠部分的面积是△BDP的面积的![]() .
.