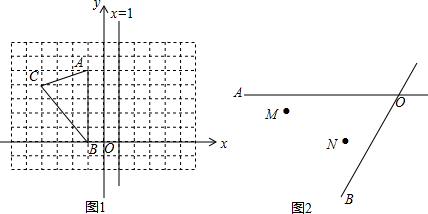
题目内容
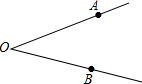 (与现实生活联系的应用题)如图,O为码头,A,B两个灯塔与码头的距离相等,OA,OB为海岸线,一轮船离开码头,计划沿∠AOB的平分线航行,在航行途中,测得轮船与灯塔A和灯塔B的距离相等,试问轮船航行时是否偏离预定航线,请说明理由.
(与现实生活联系的应用题)如图,O为码头,A,B两个灯塔与码头的距离相等,OA,OB为海岸线,一轮船离开码头,计划沿∠AOB的平分线航行,在航行途中,测得轮船与灯塔A和灯塔B的距离相等,试问轮船航行时是否偏离预定航线,请说明理由.考点:全等三角形的应用
专题:应用题
分析:只要证明轮船与O点的连线平分∠AOB就说明轮船没有偏离航线,也就是证明∠AOD=∠BOD,证角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.
解答: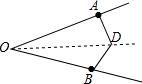 解:此时轮船没有偏离航线.
解:此时轮船没有偏离航线.
理由:由题意知:假设轮船在D处,则DA=DB,AO=BO,
在△ADC和△BDC中,
,
∴△ADO≌△BDO(SSS),
∴∠AOD=∠BOD,
即DO为∠AOB的角平分线,
∴此时轮船没有偏离航线.
 解:此时轮船没有偏离航线.
解:此时轮船没有偏离航线.理由:由题意知:假设轮船在D处,则DA=DB,AO=BO,
在△ADC和△BDC中,
|
∴△ADO≌△BDO(SSS),
∴∠AOD=∠BOD,
即DO为∠AOB的角平分线,
∴此时轮船没有偏离航线.
点评:本题考查了全等三角形的应用,解答本题的关键是:根据条件设计三角形全等,巧妙地借助两个三角形全等,寻找对应角相等.要学会把实际问题转化为数学问题来解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法,不正确的是( )
| A、0没有倒数 |
| B、0是最小的整数 |
| C、0既不是正数,也不是负数 |
| D、0是最大的非正有理数 |
下列四组线段中,可以构成直角三角形的是( )
| A、a=10,b=20,c=30 |
| B、a=20,b=30,c=40 |
| C、a=30,b=40,c=50 |
| D、a=40,b=50,c=60 |
下列说法正确的是( )
A、在球的体积公V=
| ||||
| B、若变量x、y满足y2=x,则y是x的函数 | ||||
C、在圆锥的体积公式V=
| ||||
D、若变量x、y满足y=-
|