题目内容
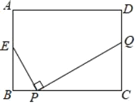
【题目】如图，矩形ABCD中，AB＝6，BC＝8，E为AB的中点，P为BC上一动点，作PQ⊥EP交直线CD于点Q，设点P每秒以1个单位长度的速度从点B运动到点C停止，在此时间段内，点Q运动的平均速度为每秒_____个单位．
【答案】
【解析】
由题意可证△BEP∽△CPQ，可得
，即CQ＝
＝
，即可求CQ的最大值，则可求点Q运动的平均速度．
解：∵四边形ABCD是矩形
∴AB＝CD＝6，∠B＝∠C＝90°，
∴∠BEP+∠BPE＝90°
∵E为AB的中点，
∴BE＝3
∵PQ⊥EP
∴∠BPE+∠CPQ＝90°，
∴∠BEP＝∠CPQ，且∠B＝∠C＝90°
∴△BEP∽△CPQ
∴
∴CQ＝＝
∴CQ的最大值为
∴点Q路程＝2×＝
∴点Q运动的平均速度＝÷（8÷1）＝
故答案为：
练习册系列答案
相关题目
【题目】某公司欲招聘一名公务人员，对甲、乙两位应试者进行了面试和笔试，他们的成绩（百分制）如表所示：
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
（1）如果公司认为面试和笔试同等重要，从他们的成绩看，谁将被录取？
（2）如果公司认为作为公务人员面试成绩应该比笔试成绩更重要，并分别赋予它们6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？
