题目内容
如图，分别以Rt△ABC的直角边AC，BC为边，在Rt△ABC外作两个等边三角形△ACE和△BCF，连接BE，AF，则∠θ的度数是________°．
120
分析：首先证明△CEB≌△CAF得到∠1=∠2，再根据三角形的内角等于与它不相邻的两个外角的和可得∠θ=∠AFB+∠FBE=∠AFB+∠CBF+∠2，再利用等量代换用∠1换∠2可得到∠θ=∠CBF+∠CFB=120°．
解答：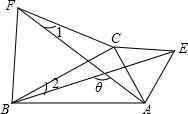
解：∵△ACE和△BCF是等边三角形，
∴∠ACE=∠FCB=∠CBF=60°，CE=AC，CF=CB，
∴∠ACF=∠ECB=60°+∠ACB．
在△CEB与△CAF中，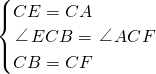
，
∴△CEB≌△CAF（SAS），
∴∠1=∠2，
∵∠θ=∠AFB+∠FBE，
∴∠θ=∠AFB+∠CBF+∠2=∠AFB+∠CBF+∠1=∠CBF+∠CFB=60°+60°=120°，
故答案为：120°．
点评：此题主要考查了全等三角形的判定与性质，解决此题的关键是证明∠1=∠2，找到∠θ=∠AFB+∠FBE．
分析：首先证明△CEB≌△CAF得到∠1=∠2，再根据三角形的内角等于与它不相邻的两个外角的和可得∠θ=∠AFB+∠FBE=∠AFB+∠CBF+∠2，再利用等量代换用∠1换∠2可得到∠θ=∠CBF+∠CFB=120°．
解答：
解：∵△ACE和△BCF是等边三角形，∴∠ACE=∠FCB=∠CBF=60°，CE=AC，CF=CB，
∴∠ACF=∠ECB=60°+∠ACB．
在△CEB与△CAF中，
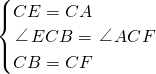，∴△CEB≌△CAF（SAS），
∴∠1=∠2，
∵∠θ=∠AFB+∠FBE，
∴∠θ=∠AFB+∠CBF+∠2=∠AFB+∠CBF+∠1=∠CBF+∠CFB=60°+60°=120°，
故答案为：120°．
点评：此题主要考查了全等三角形的判定与性质，解决此题的关键是证明∠1=∠2，找到∠θ=∠AFB+∠FBE．
练习册系列答案
相关题目
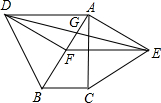如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，DE，AB相交于点G，若∠BAC=30°，下列结论：①EF⊥AC；②四边形ADFE为平行四边形；③AD=4AG；④△DBF≌△EFA．其中正确结论的序号是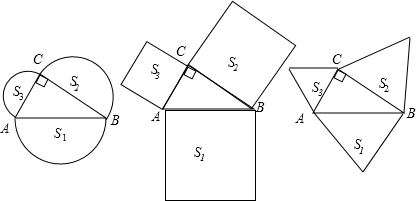
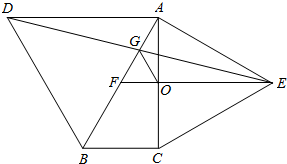如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，连接DF、EF、DE，EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：
如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB中点，连接DF、EF，DE、EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：①△DBF≌△EFA；②AD=AE；③EF⊥AC；④AD=4AG；⑤△AOG与△EOG的面积比为1：4．其中正确的结论的序号是
如图，分别以Rt△ABC三边为边向外作三个正方形，其面积分别用S1、S2、S3表示，容易得出S1、S2、S3之间有的关系式