题目内容
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一动点(与点
边上一动点(与点![]() 不重合),连接
不重合),连接![]() 将
将![]() 的两边所在射线
的两边所在射线![]() 以点
以点![]() 为中心,顺时针旋转
为中心,顺时针旋转![]() 分别交射线
分别交射线![]() 于点
于点![]() .
.
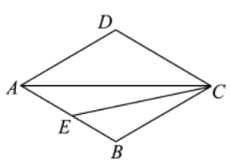
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示) ;
的式子表示) ;
(3)用等式表示线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)详情见解析;(2)∠AFC=α+30°;(3)AF+AE=![]() CG,证明见解析
CG,证明见解析
【解析】
(1)按照要求,利用旋转的性质得出对应点的位置,从而得出答案即可;
(2)利用旋转性质得出∠ECF=∠ACG=120°,由此进一步求出∠ACE=∠FCG=α,然后结合菱形的选择可知∠DAC=∠BAC=30°,据此进一步求出答案即可;
(3)作CH⊥AG于点H,首先证明△ACE与△GCF全等,由此进一步得出HG=CG×cos∠CGH,据此进一步求得AG=![]() CG,进而得出答案即可.
CG,进而得出答案即可.
(1)补全的图形如图所示:
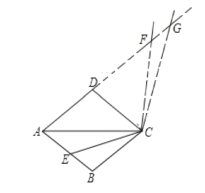
(2)由旋转性质可得:∠ECF=∠ACG=120°,
∴∠ACE+∠ACF=∠ACF+∠FCG,
∴∠ACE=∠FCG=α,
∵四边形ABCD为菱形,∠DAB=60°,
∴∠DAC=∠BAC=30°,
∴∠AGC=30°,
∴∠AFC=α+30°;
(3)线段![]() 与
与![]() 之间的数量关系为:AF+AE=
之间的数量关系为:AF+AE=![]() CG,证明如下:
CG,证明如下:
如图,作CH⊥AG于点H,
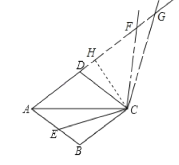
由(2)可得:∠BAC=∠DAC=∠AGC=30°,
∴CA=CG,
∴HG=![]() AG,
AG,
在△ACE与△GCF中,
∵∠ACE=∠GCF,CA=CG,∠CAE=∠CGF,
∴△ACE△GCF(ASA),
∴AE=FG,
在Rt△HCG中,
HG=CG×cos∠CGH=![]() CG,
CG,
∴AG=![]() CG,
CG,
即:AF+AE=AF+FG=AG=![]() CG,
CG,
∴线段![]() 与
与![]() 之间的数量关系为:AF+AE=
之间的数量关系为:AF+AE=![]() CG.
CG.

练习册系列答案
相关题目