题目内容
如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2。动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可
运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动。连接FM、
FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW。设动点
M、N的速度都是1个单位/秒,M、N运动的时间为x秒。试解答下列问题:
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段)。试问x为何值时,△PQW为直角三角形?
当x在何范围时,△PQW不为直角三角形?
(3)问当x为何值时,线段MN最短?求此时MN的值。


(1)提示:∵PQ∥FN,PW∥MN ∴∠QPW =∠PWF,∠PWF ="∠MNF "
∴∠QPW ="∠MNF"
同理可得:∠PQW =∠NFM或∠PWQ ="∠NFM " ∴△FMN∽△QWP
(2)当 时,△PQW为直角三角形;
时,△PQW为直角三角形;
当0≤x< ,
, <x<4时,△PQW不为直角三角形。(3)
<x<4时,△PQW不为直角三角形。(3) 解析:
解析:
略
∴∠QPW ="∠MNF"
同理可得:∠PQW =∠NFM或∠PWQ ="∠NFM " ∴△FMN∽△QWP
(2)当
 时,△PQW为直角三角形;
时,△PQW为直角三角形;当0≤x<
 ,
, <x<4时,△PQW不为直角三角形。(3)
<x<4时,△PQW不为直角三角形。(3) 解析:
解析:略

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 5、把一副三角板按如图方式放置,则两条斜边所形成的钝角α=( )
5、把一副三角板按如图方式放置,则两条斜边所形成的钝角α=( )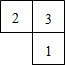 5、如图是由几个小立方块所搭成的几何体的俯视图,小正方形体的数字表示该位置小立方块的个数,则该几何体的主视图是( )
5、如图是由几个小立方块所搭成的几何体的俯视图,小正方形体的数字表示该位置小立方块的个数,则该几何体的主视图是( ) 如图,由几个小立方块所搭成的几何体,则这个几何体的主视图是( )
如图,由几个小立方块所搭成的几何体,则这个几何体的主视图是( ) 如图,已知数轴上A、B两点所表示的数分别为-2和8.则线段AB的长为( )
如图,已知数轴上A、B两点所表示的数分别为-2和8.则线段AB的长为( ) 根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.
根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.