题目内容
如图所示,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从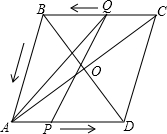 A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB-BA向点A做匀速运动.
A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB-BA向点A做匀速运动.
(1)菱形ABCD的边长为______;
(2)若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式;
②当t为何值时,S有最大值,最大值是多少?
(3)若点Q的速度为每秒a个单位长(a≤ ),当t=4秒时,△APQ是等腰三角形,请直接写出a的值.
),当t=4秒时,△APQ是等腰三角形,请直接写出a的值.
解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,且AC与BD互相平分,
∵AC=8,BD=6,
∴OA=4,OB=3,
∴AB= =
= =5;
=5;
(2)①当0<t≤ 时,由题意,得AP=t,点Q在BC上运动,
时,由题意,得AP=t,点Q在BC上运动,
如图1,过点B作BE⊥AD,垂足为E,
∵AC=8,BD=6,
∴ AD•BE=
AD•BE= AC•BD,
AC•BD,
由题意可得BE= ,
,
∴S= AP•BE,即S=
AP•BE,即S= t;
t;
②当 ≤t<5时,点Q在BA上运动,
≤t<5时,点Q在BA上运动,
由题意,得AP=t,AQ=10-2t.
如图2,过点Q作QG⊥AD,垂足为G,则QG∥BE,
∴△AQG∽△ABE,
∴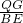 =
=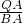 ,
,
∴QG= -
-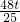 ,
,
∴S= AP•QG,
AP•QG,
即S=- t2+
t2+ t(
t( )(
)( ≤t<5).
≤t<5).
当0≤t< 时,S=
时,S= t•4
t•4
当t= 时,S的最大值为6;
时,S的最大值为6;
当 ≤t<5时,S=-
≤t<5时,S=- t2+
t2+ t,即S=-
t,即S=- (t-
(t- )2+6.
)2+6.
∴当t= 时,S的最大值为6.
时,S的最大值为6.
综上所述,当t= 时,S有最大值,最大值为6.
时,S有最大值,最大值为6.
(3)a=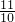 .
.
∵a≤ ,
,
∴点Q在CB上,
由题意可知PQ≥BE>PA,
∴当QA=QP时,△APQ是等腰三角形.
如图3,过点Q作QM⊥AP,垂足为点M,QM交AC于点F,
则AM= AP=2.由△AMF∽△AOD∽△CQF,
AP=2.由△AMF∽△AOD∽△CQF,
得 =
=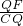 =
= =
= ,
,
∴FM= ,
,
∴QF=MQ-FM= ,
,
∴CQ=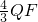 =
= .
.
则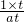 =
=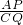 ,
,
∴a=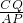 =
=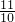 .
.
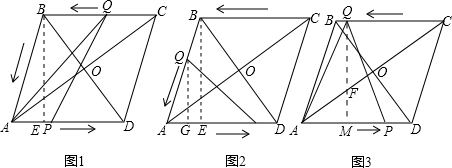
分析:(1)根据菱形的性质可知AC⊥BD,且AC与BD互相平分,再根据勾股定理即可求出菱形的边长;
(2)①当0<t≤ 时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;
时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;
②当 ≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;
≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;
(3)先判断出等腰三角形的两腰长,过点Q作QM⊥AP,垂足为点M,QM交AC于点F,根据△AMF∽△AOD∽△CQF,可得出FM的值,由QF=MQ-FM得出QF的值,进而可得出a的值.
点评:本题考查的是相似三角形的性质、菱形的性质、二次函数的最值及等腰三角形的性质,根据题意作出辅助线,利用数形结合求解是解答此题的关键.
∴AC⊥BD,且AC与BD互相平分,
∵AC=8,BD=6,
∴OA=4,OB=3,
∴AB=
 =
= =5;
=5;(2)①当0<t≤
 时,由题意,得AP=t,点Q在BC上运动,
时,由题意,得AP=t,点Q在BC上运动,如图1,过点B作BE⊥AD,垂足为E,
∵AC=8,BD=6,
∴
 AD•BE=
AD•BE= AC•BD,
AC•BD,由题意可得BE=
 ,
,∴S=
 AP•BE,即S=
AP•BE,即S= t;
t;②当
 ≤t<5时,点Q在BA上运动,
≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t.
如图2,过点Q作QG⊥AD,垂足为G,则QG∥BE,
∴△AQG∽△ABE,
∴
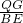 =
=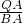 ,
,∴QG=
 -
-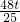 ,
,∴S=
 AP•QG,
AP•QG,即S=-
 t2+
t2+ t(
t( )(
)( ≤t<5).
≤t<5).当0≤t<
 时,S=
时,S= t•4
t•4当t=
 时,S的最大值为6;
时,S的最大值为6;当
 ≤t<5时,S=-
≤t<5时,S=- t2+
t2+ t,即S=-
t,即S=- (t-
(t- )2+6.
)2+6.∴当t=
 时,S的最大值为6.
时,S的最大值为6.综上所述,当t=
 时,S有最大值,最大值为6.
时,S有最大值,最大值为6.(3)a=
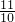 .
.∵a≤
 ,
,∴点Q在CB上,
由题意可知PQ≥BE>PA,
∴当QA=QP时,△APQ是等腰三角形.
如图3,过点Q作QM⊥AP,垂足为点M,QM交AC于点F,
则AM=
 AP=2.由△AMF∽△AOD∽△CQF,
AP=2.由△AMF∽△AOD∽△CQF,得
 =
=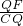 =
= =
= ,
,∴FM=
 ,
,∴QF=MQ-FM=
 ,
,∴CQ=
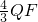 =
= .
.则
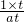 =
=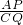 ,
,∴a=
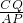 =
=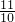 .
.
分析:(1)根据菱形的性质可知AC⊥BD,且AC与BD互相平分,再根据勾股定理即可求出菱形的边长;
(2)①当0<t≤
 时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;
时,由题意,得AP=t,点Q在BC上运动,过点B作BE⊥AD,垂足为E,由直角三角形的性质求出BE的长,由三角形的面积公式可得到S与t的关系式;②当
 ≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;
≤t<5时,点Q在BA上运动,由题意,得AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,则QG∥BE,可得出△AQG∽△ABE,由相似三角形的对应边成比例即可得出S关于t的关系式,再根据二次函数的最值问题进行解答即可;(3)先判断出等腰三角形的两腰长,过点Q作QM⊥AP,垂足为点M,QM交AC于点F,根据△AMF∽△AOD∽△CQF,可得出FM的值,由QF=MQ-FM得出QF的值,进而可得出a的值.
点评:本题考查的是相似三角形的性质、菱形的性质、二次函数的最值及等腰三角形的性质,根据题意作出辅助线,利用数形结合求解是解答此题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 7、如图所示,在菱形ABCD中,AC、BD相交于点O,E为AB中点,若OE=3,则菱形ABCD的周长是( )
7、如图所示,在菱形ABCD中,AC、BD相交于点O,E为AB中点,若OE=3,则菱形ABCD的周长是( ) 如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.
如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍. (2012•保定二模)如图所示,在菱形ABCD中,点E,F分别为AB,AC的中点,菱形ABCD的周长为32,则EF的长等于( )
(2012•保定二模)如图所示,在菱形ABCD中,点E,F分别为AB,AC的中点,菱形ABCD的周长为32,则EF的长等于( ) 如图所示,在菱形ABCD中,AC、BD相交于O,且AC:BD=1:
如图所示,在菱形ABCD中,AC、BD相交于O,且AC:BD=1: 如图所示,在菱形ABCD中,AB=AC=3cm,求∠BCD的大小和菱形的周长.
如图所示,在菱形ABCD中,AB=AC=3cm,求∠BCD的大小和菱形的周长.