ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЖдгкЕу![]() КЭ
КЭ![]() ЃЌИјГіШчЯТЖЈвхЃК
ЃЌИјГіШчЯТЖЈвхЃК
ШчЙћ ЃЌФЧУДГЦЕу
ЃЌФЧУДГЦЕу![]() ЮЊЕу
ЮЊЕу![]() ЕФЁААщЫцЕуЁБЃЎ
ЕФЁААщЫцЕуЁБЃЎ
Р§ШчЃКЕу![]() ЕФЁААщЫцЕуЁБЮЊЕу
ЕФЁААщЫцЕуЁБЮЊЕу![]() ЃЛЕу
ЃЛЕу![]() ЕФЁААщЫцЕуЁБЮЊЕу
ЕФЁААщЫцЕуЁБЮЊЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉжБНгаДГіЕу![]() ЕФЁААщЫцЕуЁБ
ЕФЁААщЫцЕуЁБ![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ЃЈ2ЃЉЕу![]() дкКЏЪ§
дкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌШєЦфЁААщЫцЕуЁБ
ЕФЭМЯѓЩЯЃЌШєЦфЁААщЫцЕуЁБ![]() ЕФзнзјБъЮЊ2ЃЌЧѓКЏЪ§
ЕФзнзјБъЮЊ2ЃЌЧѓКЏЪ§![]() ЕФНтЮіЪНЃЎ
ЕФНтЮіЪНЃЎ
ЃЈ3ЃЉЕу![]() дкКЏЪ§
дкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌЧвЕу
ЕФЭМЯѓЩЯЃЌЧвЕу![]() Йигк
Йигк![]() жсЖдГЦЃЌЕу
жсЖдГЦЃЌЕу![]() ЕФЁААщЫцЕуЁБЮЊ
ЕФЁААщЫцЕуЁБЮЊ![]() ЃЎШєЕу
ЃЎШєЕу![]() дкЕквЛЯѓЯоЃЌЧв
дкЕквЛЯѓЯоЃЌЧв![]() ЃЌЧѓДЫЪБЁААщЫцЕуЁБ
ЃЌЧѓДЫЪБЁААщЫцЕуЁБ![]() ЕФКсзјБъЃЎ
ЕФКсзјБъЃЎ
ЃЈ4ЃЉЕу![]() дкКЏЪ§
дкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌШєЦфЁААщЫцЕуЁБ
ЕФЭМЯѓЩЯЃЌШєЦфЁААщЫцЕуЁБ![]() ЕФзнзјБъ
ЕФзнзјБъ![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌжБНгаДГіЪЕЪ§
ЃЌжБНгаДГіЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
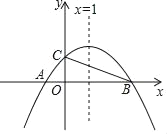
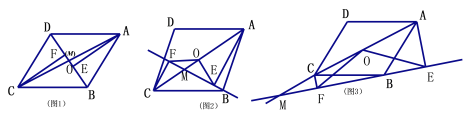
ЁОД№АИЁПЃЈ1ЃЉЕуAЃЇЕФзјБъЮЊЃЈ2ЃЌ1ЃЉЃЛЃЈ2ЃЉy=![]() x+3ЃЛЃЈ3ЃЉDЃЇЕФКсзјБъЮЊ
x+3ЃЛЃЈ3ЃЉDЃЇЕФКсзјБъЮЊ![]() ЃЛЃЈ4ЃЉЃ2ЁмnЁм0ЁЂ1ЁмnЁм3
ЃЛЃЈ4ЃЉЃ2ЁмnЁм0ЁЂ1ЁмnЁм3
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌ![]() ЃЌдђ
ЃЌдђ![]() ,МДПЩЧѓНт.
,МДПЩЧѓНт.
ЃЈ2ЃЉЗж![]() ЪБЃЌСНжжЧщПіЗжБ№ЧѓНт.
ЪБЃЌСНжжЧщПіЗжБ№ЧѓНт.
ЃЈ3ЃЉЩшЕуCЕФКсзјБъЮЊnЃЌЕуCдкКЏЪ§y=Ѓx2+4ЕФЭМЯѓЩЯЃЌCD=DDЃЇЃЌМДПЩЧѓНт.
ЃЈ4ЃЉЭЈЙ§ЛЭММДПЩЧѓНт.
НтЃКЃЈ1ЃЉЕуAЃЇЕФзјБъЮЊЃЈ2ЃЌ1ЃЉЃЎ
ЃЈ2ЃЉЂйЕБmЁн0ЪБЃЌ
m+1=2ЃЌm=1;
ЁрBЃЈ1ЃЌ2ЃЉ,
ЁпЕуBдквЛДЮКЏЪ§y=kx+3ЭМЯѓЩЯЃЌ
Ёрk+3=2ЃЌ
НтЕУЃКk=-1;
ЁрвЛДЮКЏЪ§НтЮіЪНЮЊy=-x+3;
ЂкЕБmЃМ0ЪБЃЌ
m+1=-2ЃЌm=-3;
ЁрBЃЈ-3ЃЌ-2ЃЉЃЎ
ЁпЕуBдквЛДЮКЏЪ§y=kx+3ЭМЯѓЩЯЃЌ
Ёр-3k+3=-2ЃЌ
НтЕУЃКk=![]() ЃЌ
ЃЌ
ЁрвЛДЮКЏЪ§НтЮіЪНЮЊy=![]() x+3;
x+3;
ЃЈ3ЃЉЩшЕуCЕФКсзјБъЮЊnЃЌЕуCдкКЏЪ§y=Ѓx2+4ЕФЭМЯѓЩЯЃЌ
ЁрЕуCЕФзјБъЮЊЃЈnЃЌ-n2+4ЃЉЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ-nЃЌ-n2+4ЃЉЃЌDЃЇЃЈ-nЃЌn2-4ЃЉ;
ЁпCD=DDЃЇЃЌ
Ёр2n=2ЃЈ-n2+4ЃЉЃЌ
НтЕУЃКn=![]() ;
;
ЁпЕуCдкЕквЛЯѓЯоЃЌ
ЁрШЁ![]() ЃЌ
ЃЌ![]() ЃЈЩсЃЉ;
ЃЈЩсЃЉ;
ЁрDЃЇЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉЃ2ЁмnЁм0ЁЂ1ЁмnЁм3ЃЎ
НтЮіШчЯТЃК
ЕБзѓБпЕФХзЮяЯпдкЩЯЗНЪБЃЌШчЭМЂйЁЂЭМЂкЃЎЃ2ЁмnЁм0,
ЕБгвБпЕФХзЮяЯпдкЩЯЗНЪБЃЌШчЭМЂлЁЂЭМЂмЃЎ1ЁмnЁм3;
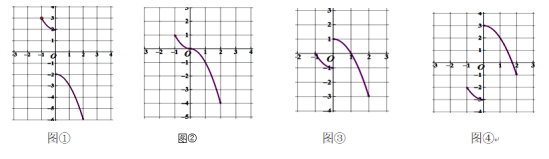

 ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
ЭЌВНЭиеЙдФЖСЯЕСаД№АИЁОЬтФПЁПЖўДЮКЏЪ§![]() ЮЊГЃЪ§ЃЌ
ЮЊГЃЪ§ЃЌ![]() жаЕФ
жаЕФ![]() гы
гы![]() ЕФВПЗжЖдгІжЕШчЯТБэЃК
ЕФВПЗжЖдгІжЕШчЯТБэЃК
x | -1 | 0 | 3 |
y | n | -3 | -3 |
ЕБ![]() ЪБЃЌЯТСаНсТлжавЛЖЈе§ШЗЕФЪЧ________(ЬюађКХМДПЩ)
ЪБЃЌЯТСаНсТлжавЛЖЈе§ШЗЕФЪЧ________(ЬюађКХМДПЩ)
Ђй![]() ЃЛЂкЕБ
ЃЛЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЫц
ЕФжЕЫц![]() жЕЕФдіДѓЖјдіДѓЃЛЂл
жЕЕФдіДѓЖјдіДѓЃЛЂл![]() ЃЛЂмЕБ
ЃЛЂмЕБ![]() ЪБЃЌЙигк
ЪБЃЌЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() ЕФНтЪЧ
ЕФНтЪЧ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ