题目内容
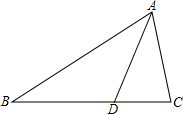 △ABC中,∠B<∠C,AD平分∠BAC
△ABC中,∠B<∠C,AD平分∠BAC
(1)在图中画出△ABC的高AE,垂足为E;并完成下列问题:
1.若∠B=50°,∠C=70°,则∠DAE=________.
2.试探寻∠DAE与∠B、∠C的关系.请说明理由.
(2)若一点F在AD上移动,且FE⊥BC于E,其他条件不变,那么∠EFD与∠B、∠C间有怎样的关系?________.
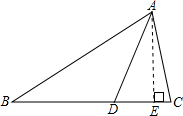 解:(1)1、∵B=50°,∠C=70°,AE⊥BC于E,
解:(1)1、∵B=50°,∠C=70°,AE⊥BC于E,∴∠BAC=60°,∠BAE=40°.
又AD平分∠BAC,
∴∠BAD=
 ∠BAC=30°.
∠BAC=30°.∴∠DAE=∠BAE-∠BAD=10°;
2、∵AE⊥BC于E,AD平分∠BAC,
∴∠DAE=90°-∠ADE
=90°-(∠B+∠BAD)
=90°-(∠B+
 ∠BAC)
∠BAC)=90°-(∠B+90°-
 ∠B-
∠B- ∠C)
∠C)=
 (∠C-∠B)
(∠C-∠B)=10°;
(2)根据题意,知点F与点A重合.
证明过程同(1)2.∴∠EFD=
 (∠C-∠B).
(∠C-∠B).故答案是:10°、∠EFD=
 (∠C-∠B).
(∠C-∠B).分析:(1)1、根据三角形的内角和定理求得∠BAC和∠BAD的度数,根据角平分线定义求得∠BAE的度数,从而求得∠DAE的度数;
2、根据三角形的内角和定理、角平分线定义可以求得∠DAE=
 (∠C-∠B);
(∠C-∠B);(2)证明过程同(1).
点评:此题综合运用了三角形的内角和定理、及角平分线定义.解答(2)时,要先确定点F的位置,再来找∠EFD与∠B、∠C间的关系.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )
如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
 如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,
如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,