题目内容
解关于x的方程:
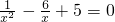
解:设 =t,则原方程可化为t2-6t+5=0,
=t,则原方程可化为t2-6t+5=0,
解方程t2-6t+5=0得t1=1,t2=5,
当t=1时,则 =1,解得x1=1,
=1,解得x1=1,
当t=5时,则 =5,解得x2=
=5,解得x2= ,
,
经检验x1=1,x2= 都是原方程的解,
都是原方程的解,
所以原方程的解为:x1=1,x2= .
.
分析:设 =t,则原方程可化为t2-6t+5=0,利用因式分解法求得t1=1,t2=5,再分别代入t=
=t,则原方程可化为t2-6t+5=0,利用因式分解法求得t1=1,t2=5,再分别代入t= 中,得到x1=1,x2=
中,得到x1=1,x2= ,然后把x1=1,x2=
,然后把x1=1,x2= 代入原方程进行检验,从而确定原方程的解.
代入原方程进行检验,从而确定原方程的解.
点评:本题考查了换元法解分式方程:先利用换元法把原分式方程转化为简单的分式方程或整式方程,然后解出简单的分式方程或整式方程,再代入换元的等式中求出原方程所含未知数的值,然后进行检验得到原分式方程的解.
 =t,则原方程可化为t2-6t+5=0,
=t,则原方程可化为t2-6t+5=0,解方程t2-6t+5=0得t1=1,t2=5,
当t=1时,则
 =1,解得x1=1,
=1,解得x1=1,当t=5时,则
 =5,解得x2=
=5,解得x2= ,
,经检验x1=1,x2=
 都是原方程的解,
都是原方程的解,所以原方程的解为:x1=1,x2=
 .
.分析:设
 =t,则原方程可化为t2-6t+5=0,利用因式分解法求得t1=1,t2=5,再分别代入t=
=t,则原方程可化为t2-6t+5=0,利用因式分解法求得t1=1,t2=5,再分别代入t= 中,得到x1=1,x2=
中,得到x1=1,x2= ,然后把x1=1,x2=
,然后把x1=1,x2= 代入原方程进行检验,从而确定原方程的解.
代入原方程进行检验,从而确定原方程的解.点评:本题考查了换元法解分式方程:先利用换元法把原分式方程转化为简单的分式方程或整式方程,然后解出简单的分式方程或整式方程,再代入换元的等式中求出原方程所含未知数的值,然后进行检验得到原分式方程的解.

练习册系列答案
相关题目
解关于x的方程
=
产生增根,则常数m的值等于( )
| x-3 |
| x-1 |
| m |
| x-1 |
| A、-1 | B、-2 | C、1 | D、2 |