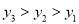题目内容
完成下面的证明:
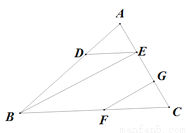
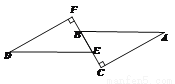
如图,已知DE∥BC,∠DEB=∠GFC,试说明BE∥FG.
【解析】
∵DE∥BC
∴∠DEB=______( ).
∵∠DEB=∠GFC
∴______=∠GFC ( ).
∴BE∥FG( ).
∠1,两直线平行内错角相等,∠1,等量代换,同位角相等两直线平行. 【解析】试题分析:由两直线平行内错角相等得∠DEB=∠1,由等量代换得∠1=∠GFC,再由同位角相等两直线平行 得BE∥FG. 试题解析:∵DE∥BC ∴∠DEB=∠1( 两直线平行内错角相等 ). ∵∠DEB=∠GFC ∴∠1=∠GFC (等量代换 ). ∴BE∥FG( 同位角相等两直线平行 ...已知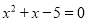 ,则代数式
,则代数式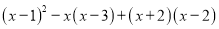 的值为__________.
的值为__________.
计算: 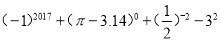
《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为__________________.

两个同样的直角三角板如图所示摆放,使点F,B,E,C在一条直线上,则有DF∥AC,理由是_____.
已知x,y是有理数,且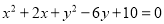 ,则
,则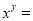 _________.
_________.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
列方程组解应用题
新年联欢会上,同学们组织了猜谜活动,并采取每答对一题得分,每答错一题扣分记分方法。王强答对7道题,答错3道题共获得50分;李想答对8道题,答错1道题,共获得62分。问答对一题得多少分,答错一题扣多少分。
答对道题得8分,答错一道题扣2分. 【解析】试题分析:设答对一题得x分,答错一道题扣y分,根据"答对7道题,答错3道题共获得50分,答对8道题,答错1道题,共获得62分"列二元一次方程组即可. 试题解析:设答对一题得x分,答错一道题扣y分, 由题意得: 解得: 答:答对一题得8分,答错一道题扣2分。已知:如图,DE平分∠BDF,∠A=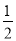 ∠BDF,DE
∠BDF,DE BF,求证:AC
BF,求证:AC BF
BF
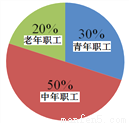
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数

表2:小王抽样调查单位10名职工的健康指数

表3:小李抽样调查单位10名职工的健康指数

根据上述材料回答问题:
(1)扇形统计图中老年职工所占部分的圆心角度数为
(2)小张、小王和小李三人中, 的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
查看答案解不等式组 并求出它的非负整数解.
并求出它的非负整数解.
解方程组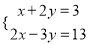
完成下面的证明:

如图,已知DE∥BC,∠DEB=∠GFC,试说明BE∥FG.
【解析】
∵DE∥BC
∴∠DEB=______( ).
∵∠DEB=∠GFC
∴______=∠GFC ( ).
∴BE∥FG( ).
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知x,y是有理数,且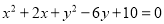 ,则
,则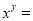 _________.
_________.
一个角的补角等于这个角的3倍,则这个角的度数为_____________.
查看答案计算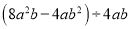 结果为_____________.
结果为_____________.
因式分【解析】
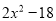 =______.
=______.
用小棋子摆出如下图形,则第n个图形中小棋子的个数为( )
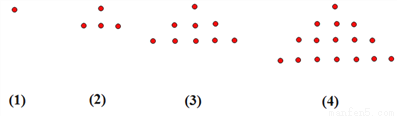
A. n B. 2n C. n2 D. n2+1
查看答案某市居民用电的电价实行阶梯收费,收费标准如下表:
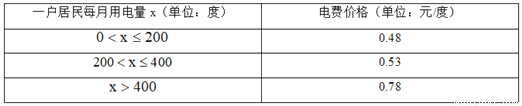
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,直接写出李叔家七月份最多可用电的度数是( )
A. 100 B. 396 C. 397 D. 400
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
小文统计了本班同学一周的体育锻练情况,并绘制了直方图
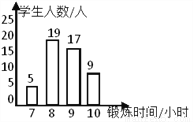
①小文同学一共统计了60人;
②这个班同学一周参加体育锻炼时间的众数是8;
③这个班同学一周参加体育锻炼时间的中位数是9;
④这个班同学一周参加体育锻炼时间的平均值为8.
根据图中信息,上述说法中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
B 【解析】小文同学一共统计了5+19+17+9=50人,故①错; 数据8出现了19次,最多,为众数,故②正确; 在第25位,26位的均是9,所以9为中位数,③正确; 这个班同学一周参加体育锻炼时间的平均值为(5×7+19×8+17×9+9×10)=8.6, ④错; 故选:B.下列因式分解正确的是( )
A. 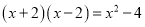 B.
B. 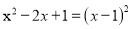
C. 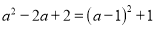 D.
D. 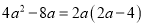
若把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )
A.  B.
B. 
C. 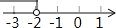 D.
D. 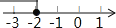
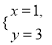 是二元一次方程
是二元一次方程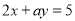 的一个解,则a的值为( )
的一个解,则a的值为( )
A. 1 B. 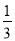 C. 3 D. -1
C. 3 D. -1
下列计算正确的是( )
A. 2a+3a=6a B. a2+a3=a5 C. a8÷a2=a6 D. (a3)4= a7
查看答案已知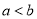 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A. 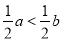 B.
B. 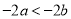 C.
C. 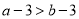 D.
D. 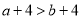
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是_____%.
20 【解析】设该药品平均每次降价的百分率为x,根据降价后的价格=降价前的价格(1-降价的百分率),则第一次降价后的价格是25(1-x),第二次后的价格是25(1-x)2,据此即可列方程求解. 【解析】 设该药品平均每次降价的百分率为x, 由题意可知经过连续两次降价,现在售价每盒16元, 故25(1-x)2=16, 解得x=0.2或1.8(不合题意,舍去), 故该药品平均每次...已知抛物线y=ax2-3x+c(a≠0)经过点(-2,4),则4a+c-1=____.
查看答案若一元二次方程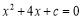 有两个不相等的实数根,则c的值可以是 (写出一个即可).
有两个不相等的实数根,则c的值可以是 (写出一个即可).
抛物线y=2x2﹣3x+4与y轴的交点坐标是______.
查看答案如图是二次函数y=ax2+bx+c过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac,②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( )
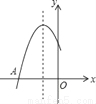
A. ②④ B. ①④ C. ②③ D. ①③
查看答案设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
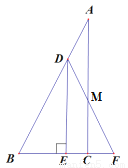
如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm2?
(2)△PAQ的面积能否达到3cm2?
(3)经过多长时间,P、Q两点之间的距离为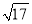 cm?
cm?
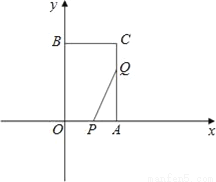
如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
查看答案甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
查看答案已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
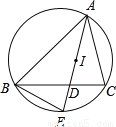
查看答案如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.求证:IE=BE.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


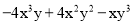
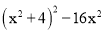
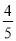 x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )
x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )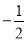 ,y1)、N(
,y1)、N(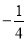 ,y2)、P(
,y2)、P(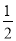 ,y3)三点都在函数
,y3)三点都在函数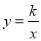 (k﹤0)的图象上,则y1、y2、y3的大小关系是( )
(k﹤0)的图象上,则y1、y2、y3的大小关系是( ) B.
B.  C.
C.  D.
D.