题目内容
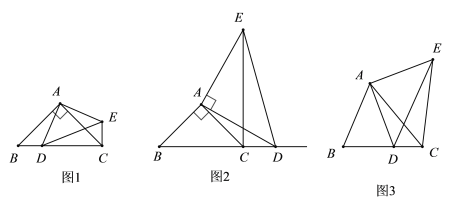
【题目】如图AB∥CD,点P是平面内直线AB、CD外一点连接PA、PC。
(1)写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系;
(2)证明图(1)和图(3)的结论。

【答案】(1)图1,∠APC+∠A+∠C=360°;图2,∠APC=∠A+∠C;图3,∠C=∠A+∠APC;图4,∠A=∠C+∠APC;(2)证明图1见解析;证明图3见解析.
【解析】
1)依据图形可得∠APC、∠PAB、∠PCD之间的数量关系;
(2)过P作PE∥AB,即可得到PE∥CD,再根据平行线的性质以及角的和差关系,即可得出∠PCD=∠CPE,∠PAB=∠APE,利用三角形的外角的性质,得出∠C=∠A+∠APC.
(1)图1,∠APC+∠A+∠C=360°;图2,∠APC=∠A+∠C;图3,∠C=∠A+∠APC;图4,A=∠C+∠APC.
(2)证明图1:

如图,过P点作,PE∥AB,则:∠A+∠APE=180°,
∵AB∥CD,
∴PE∥CD
∴∠EPC+∠C=180°.
又∵∠APC=∠APE+∠EPC,
∴∠APC+∠A+∠C=360°;
证明图3:过P作PE∥AB,
∵AB∥CD,
∴PE∥CD,
∴∠PCD=∠CPE,∠PAB=∠APE,
∴∠APC=∠CPE-∠APE=∠C-∠A,即∠C=∠A+∠APC

练习册系列答案
相关题目